If AD, BE, CF are the diameters of circumcircle of ΔABC, then prove that area of hexagon AFBDCE is 2Δ
Text Solution
Chord AC subtends the same angle at point B and D
∴Ang≤ADC=B
So, in right angled triangled ACD
CD=ACcotB
∴CD=bcotB
Similarly from ΔABD,
BD=ccotC

∴ Area of ΔBDC
ΔBDC=12(bcotB)(ccotC)sin(B+C)
=bc2sinAcotCcotB
=abc4RcotBcotC
Similarly ΔAEC=abc4RcotAcotC
and ΔAFB=abc4RcotAcotB
∴ Area of hexagon AFBDCE
=ΔBDC+ΔAFC+ΔAFB+ΔABC
=abc4R[cotAcotB+cotBcotC+cotCcotA]+Δ
=Δ+Δ
(as in ΔABC,cotAcotB+cotBcotC+cotA=1)
=2Δ
|
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.8
7 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.9
5 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.6
6 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
32 Videos
Similar Questions
Knowledge Check
If R is the radius of the circumcircle of the ΔABCandΔ is its area then
AR=a+b+c2BR=a+b+cΔCR=abc4ΔDR=abcΔIf O is the centroid and AD, BE and CF are the three medians of ΔABC with an area of 96cm2 then the area of ΔBOD in cm2 is
A8B12C16D24If AD, BE, CF are the altitudes of ΔABC whose orthocentre is H, then C is the orthocentre of :
A△ABHB△BDHC△ABDD△BEA
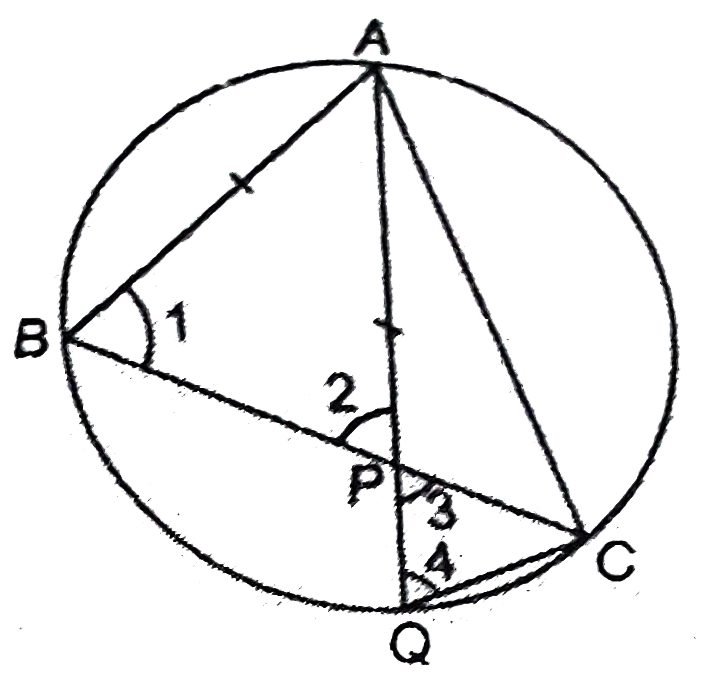
In given figure , ABC is a triangle produced meets the circumcircle of ΔABC at Q, prove that CP=CQ
View SolutionFind the ratio of area of ΔADE to Δ ABC

View Solution
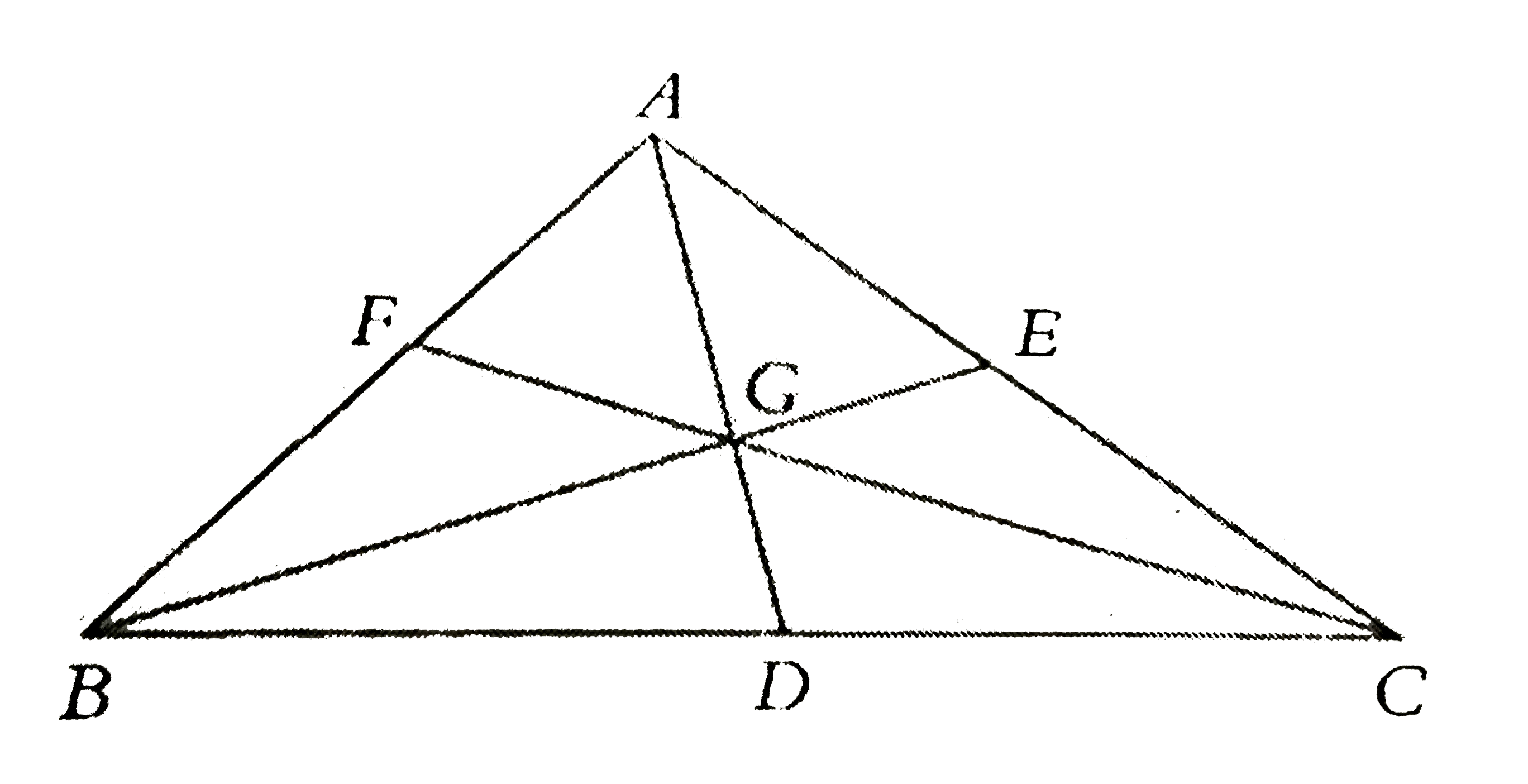
In the above ΔABC,¯¯¯¯¯¯AD,¯¯¯¯¯¯BE,and¯¯¯¯¯¯CF are the medians. G is the centroid. What is the ratio of the areas of ΔBGDandΔGCE?
View SolutionIn the given ΔABC,¯¯¯¯¯¯AD,¯¯¯¯¯¯BE and ¯¯¯¯¯¯CF are the medians. G is centroid. What is the ratio of the area of ΔBGD and ΔGCE?
View SolutionIn a ΔABC,AD,BE and CF are three medians. The perimeter of ΔABC is always.
View Solution
