The resultant of $\to A and \to B$ makes an angle $α$ with $\to A$ and $β and \to B$ ,

Video Solution

Text Solution

Verified by Experts

The correct Answer is:3

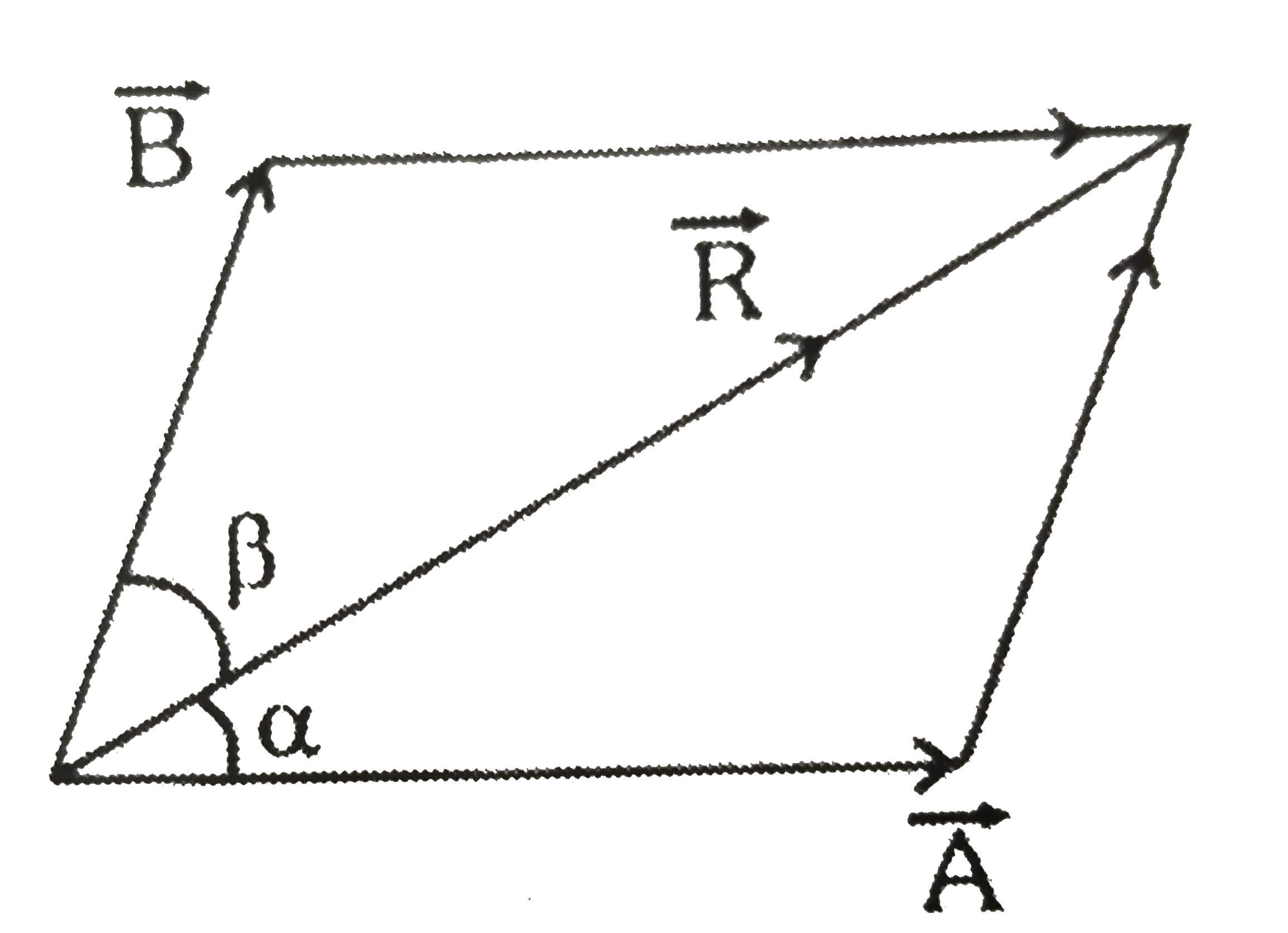
Resultant is inclined towards vector of large magnitude thus. If $A > B$ then alpha lt beta.

|

Updated on:21/07/2023

Class 11 PHYSICS BASIC MATHEMATICS USED IN PHYSICS &VECTORS

Topper's Solved these Questions

BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - RESOLUTION OF VECTOR
8videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - DOT PRODUCT
20videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - DEFINITION & TYPES OF VECTOR
6videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19videos
CENTRE OF MASS

Similar Questions

Knowledge Check

Question 1 - Select One
The resultant of $\to A$ and $\to B$ makes an angle $α$ with $\to A and \to β$ with $\to B$ , then -
A $α < β$
B $α < β if A < B$
C $α < β if A > B$
D $α < β if A = B$
Question 2 - Select One
If the resultant of $\to A$ and $\to B$ makes angle $α$ with $\to A$ and $β$ with $\to B$ , then
A $α < β$ always
B $α < β$ if $A < B$
C $α < β$ if $A > B$
D $α < β$ if A=B
Question 3 - Select One
Two vectors $\to A and \to B$ inclined at an angle $θ$ have a resultant $\to R$ which makes an angle $α$ with $\to A$ and angle $β$ with $\to B$ . Let the magnitudes of the vectors $\to A, \to B and \to R$ be represented by A, B and R respectively. Which of the following relations is not correct ?
A $\frac{R}{sin (α + β)} = \frac{A}{sin α} = \frac{B}{sin β}$
B $R sin α = B sin (α + β)$
C $A sin α = B sin β$
D $R sin β = A sin (α + β)$

ALLEN-BASIC MATHEMATICS USED IN PHYSICS &VECTORS -ADDITON & SUBTRACTION, MULTIPLICATION & DIVISION OF A VECTOR BY A SCALAR

Home
Ask Doubt
Profile