Doubtnut Promotions Sticky

In vector diagram shown in figure where (→R) is the resultant of vectors (→A)and(→B).
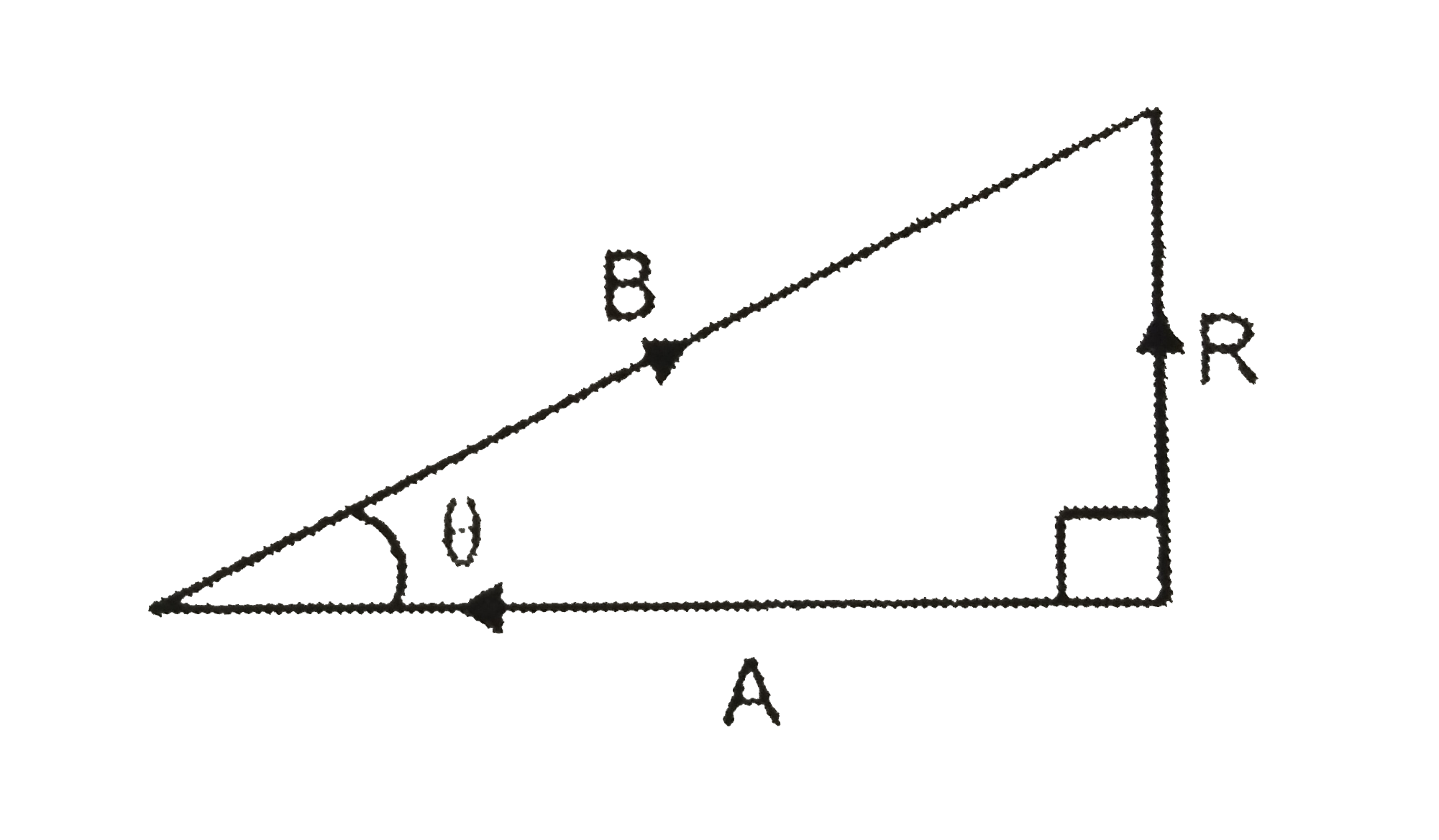
In vector diagram shown in figure where (vecR) is the resultant of vectors (vecA) and (vecB). If R= (B)/(sqrt2), then value of angle theta is :
If R=B√2, then value of angle θ is :

A

30∘

B

45∘

C

60∘

D

75∘

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

ocr_image
sinθ=RB=B/√2B=1√2⇒θ=45∘

|
Updated on:21/07/2023
Class 11PHYSICSBASIC MATHEMATICS USED IN PHYSICS &VECTORS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    In vector diagram shown in figure where (→R) is the resultant of vectors (→A) and (→B). If R=B√2, the value of angle θ is :
    ocr_image

    A30∘
    B45∘
    C60∘
    D75∘
  • Question 2 - Select One

    →R is the resultant of →A and →B . →R is inclined to →A at angle theat1 and to →B at angle θ2, then :

    Aθ1<θ2
    Bθ1<θ2ifA>B
    Cθ1<θ2ifA<B
    Dθ1<θ2ifA=B
  • Question 3 - Select One

    The vector sum of two vectors →Aand→B is maximum , then the angle θ between two vector is

    A0∘
    B30∘
    C45∘
    D60∘