Triangles ABC and ABD are isosceles with AB=AC=BD,and¯¯¯¯¯¯BD intersects ¯¯¯¯¯¯AC at E. If ¯¯¯¯¯¯BD⊥¯¯¯¯¯¯AC then ∠C+∠D is
Step by step video & image solution for Triangles ABC and ABD are isosceles with AB = AC = BD, and bar(BD) intersects bar(AC) at E. If bar(BD) _|_ bar(AC) then /_C+ /_D is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Triangles ABC and ABD are isosceles with AB=AC=BD,and¯¯¯¯¯¯BD intersects ¯¯¯¯¯¯AC at E. If ¯¯¯¯¯¯BD⊥¯¯¯¯¯¯AC then ∠C+∠D is
View SolutionConsider all triangels ABC satisfying the following conditions : AB = AC, D is a point on ¯¯¯¯¯¯AC for which ¯¯¯¯¯¯BD⊥¯¯¯¯¯¯AC,AD,andCD are integers, and BD2=57. Among all such triangles, the smallest possible value of AC is
View Solution
Knowledge Check
In a ΔABC,¯¯¯¯¯¯AB2+¯¯¯¯¯¯AC2=¯¯¯¯¯¯BC2 and ¯¯¯¯¯¯BC=√2¯¯¯¯¯¯AB , then ∠ABCis :
AA)30∘BB)45∘CC)60∘DD)90∘ΔABC is an isosceles triangle and ¯¯¯¯¯¯AB=¯¯¯¯¯¯AC=2aunit, ¯¯¯¯¯¯BC = a unit. Draw AD⊥BC, and find the length of ¯¯¯¯¯¯AD .
A√15 a unitB√152 a unitC√17 a unitD√172a unit
ABC is an isosceles triangle with AB =AC and BD,CE are its two medians. Show that BD=CE .
View SolutionABC is an isosceles triangle with AB =AC and BD,CE are its two medians. Show that BD=CE .
View SolutionIn an isosceles right triangle ABC, ∠B=90∘ and ¯¯¯¯¯¯BD⊥¯¯¯¯¯¯AC.Then BD=………………(AB2/BC2/AC2).
View SolutionIf A,B,C and D are four points and ¯¯¯¯¯¯AB=¯¯¯¯¯¯DC then ¯¯¯¯¯¯AC+¯¯¯¯¯¯BD= (A) 2−−→AD (B) 2−−→CB (C) 2−−→AC (D) none
View SolutionIn Figure, ABC is an isosceles triangle with AB=AC, BD and CE are two medians of the triangle. Prove that BD=CE
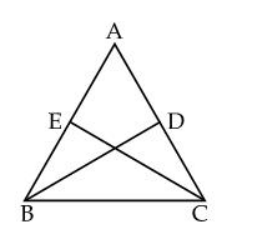
View SolutionABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACxCD. Prove that BD=BC
View Solution
