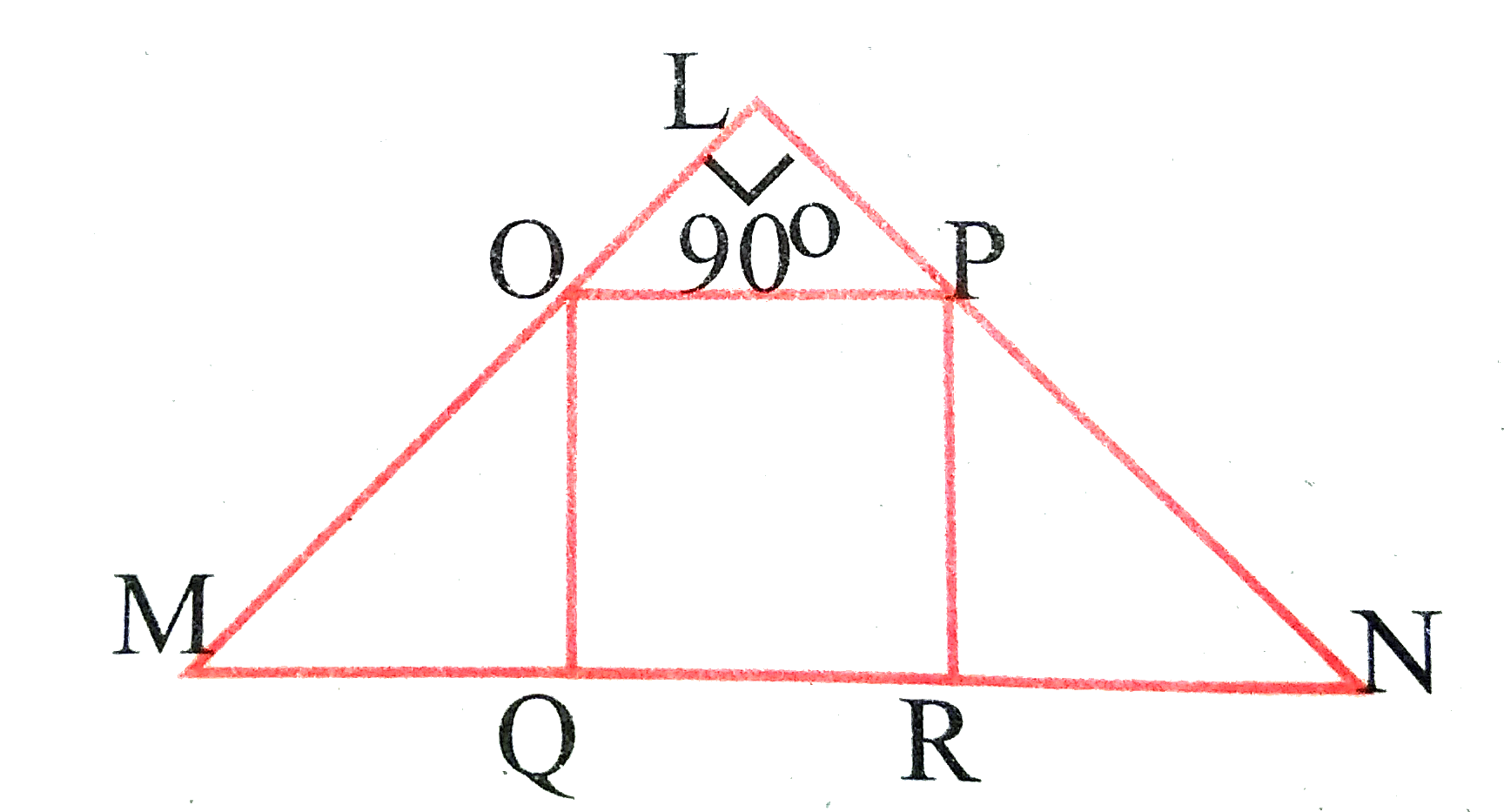
In figure OPRQ is a square and $∠ M L N = 90^{\circ}$ . Prove that
$(i) Δ L O P ~ Δ Q M O (i i) Δ L O P ~ Δ R P N$
$(i i i) Δ Q M O ~ Δ R P N (i v) Q R^{2} = M Q \times R N$ .
Solution in Tamil

Video Solution

Answer

Step by step video solution for In figure OPRQ is a square and angle MLN =90^(@). Prove that (i) Delta LOP ~ Delta QMO (ii) Delta LOP ~ Delta RPN (iii) DeltaQMO ~ Delta RPN (iv) QR^(2)=MQ xx RN. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS CIRCLES

In figure OPRQ is a square and ∠MLN=90∘. Prove that (i)ΔLOP~ΔQMO(ii)ΔLOP~ΔRPN (iii)ΔQMO~ΔRPN(iv)QR2=MQ×RN. Solution in Tamil

Topper's Solved these Questions

Similar Questions

FULL MARKS-GEOMETRY-EXERCISE 4.1

In figure OPRQ is a square and $∠ M L N = 90^{\circ}$ . Prove that
$(i) Δ L O P ~ Δ Q M O (i i) Δ L O P ~ Δ R P N$
$(i i i) Δ Q M O ~ Δ R P N (i v) Q R^{2} = M Q \times R N$ .
Solution in Tamil