In a class, each student likes either cricket or football 40% of the students like football. 80% of the students like cricket. The number of studnets who like only cricket is 40 more than the number of students who like only football. What is the strength of the class?
80
100
120
150
The correct Answer is:B
To solve the problem step by step, we will define variables and set up equations based on the information provided.
Step 1: Define the Variables
Let the total number of students in the class be x.
Step 2: Set Up the Equations
From the problem, we know:
- 40% of the students like football:
A+B=0.4x
- 80% of the students like cricket:
B+C=0.8x
- The number of students who like only cricket (C) is 40 more than the number of students who like only football (A):
C=A+40
Step 3: Substitute the Third Equation into the First Two
Substituting C=A+40 into the second equation:
B+(A+40)=0.8x
This simplifies to:
A+B+40=0.8x
Now, we can express B in terms of A:
B=0.8x−A−40
Step 4: Substitute B into the First Equation
Now substitute B from the above equation into the first equation:
A+(0.8x−A−40)=0.4x
This simplifies to:
0.8x−40=0.4x
Rearranging gives:
0.8x−0.4x=40
0.4x=40
Step 5: Solve for x
Now, divide both sides by 0.4:
x=400.4=100
Conclusion
The strength of the class is 100 students.
Let the total number of students in the class be x.
From the problem, we know:
- 40% of the students like football:
A+B=0.4x
- 80% of the students like cricket:
B+C=0.8x
- The number of students who like only cricket (C) is 40 more than the number of students who like only football (A):
C=A+40
Substituting C=A+40 into the second equation:
B+(A+40)=0.8x
This simplifies to:
A+B+40=0.8x
Now, we can express B in terms of A:
B=0.8x−A−40
Now substitute B from the above equation into the first equation:
A+(0.8x−A−40)=0.4x
This simplifies to:
0.8x−40=0.4x
Rearranging gives:
0.8x−0.4x=40
0.4x=40
Now, divide both sides by 0.4:
x=400.4=100
The strength of the class is 100 students.
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SETS AND RELATIONSEXERCISE - LEVEL 224videos
SETS AND RELATIONS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SETS AND RELATIONSEXERCISE - LEVEL 38videos
SETS AND RELATIONS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SETS AND RELATIONSEXERCISE - Easy type5videos
SETS AND RELATIONS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SALES TAX AND COST OF LIVING INDEX EXERCISE - Level 314videos
SALES TAX AND COST OF LIVING INDEX
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SHARES AND DIVIDENDSEXERCISE - CONCEPT APPLICATION (LEVEL 3)10videos
SHARES AND DIVIDENDS
Similar Questions
In a class, each student likes either cricket or football, 40% of the students like football, 80% of the students like cricket. The number of students who like only cricket is 40 more than the number of students who like only football. Then the strength of the class is :
View SolutionOut of 30 students in a class, 20 like cricket and 10 like Hockey. The ratio of the number of students liking Hockey to the total number of students is
View Solution
Knowledge Check
- Question 1 - Select One

Find out the number of students who play only cricket.A25B18C9D41 - Question 2 - Select One
A class has 50 student ,each student likes either cricket or football or both .Sixteen students like both the games .Find the number of students who like exactly one game .
A34B32C38D36 - Question 3 - Select One
A class has 50 student ,each student likes either cricket or football or both .Sixteen students like both the games .Find the number of students who like exactly one game .
A34B32C38D36
Out of 30 students in a class, 6 like football, 12 like cricket and remaining like tennis. Find the ratio of
Number of students liking cricket to total number of students.View SolutionIf Rs. 4 becomes Rs. 10 in 50 years at simple interest, the rate % p.a. is
View SolutionIn a school 80 students like chocolate, 40 like coffee if the number of students doesn't like any of them is equal to the number of students who like both of them then what is the total number of students in the school?
View SolutionThe pie chart given below shorts the distribution of students who like the given 5 sports. The total number of students is 960.
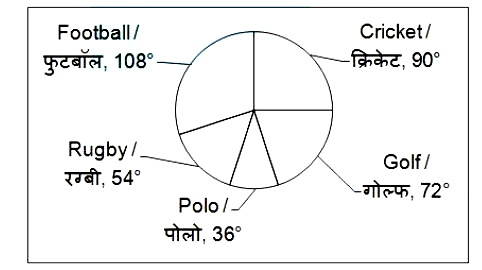
The number of students who like Golf is how much percent more than the number of students who like Rugby?View SolutionIn a class of 60 students, 40 students play cricket and only 30 students play football . The number of students who can play both cricket and football is
View Solution

