CD और GH क्रमश: ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमशः ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं । यदि ΔABC~ΔFEG हैं , तो दर्शाइए कि :
( i ) CDGH=ACFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
Step by step video & image solution for CD और GH क्रमश: angleACB और angleEGF के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमशः DeltaABC और DeltaEFG की भुजाओं AB और FE पर स्थित हैं । यदि DeltaABC ~ DeltaFEG हैं , तो दर्शाइए कि : ( i ) frac{CD}{GH}=frac{AC}{FG} (ii) DeltaDCB~DeltaHGE (iii) DeltaDCA~DeltaHGF by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिभुजEXERCISE - प्रश्नावली 6.49videos
त्रिभुज
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिभुजEXERCISE - प्रश्नावली 6.517videos
त्रिभुज
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिभुजEXERCISE - प्रश्नावली 6.210videos
त्रिभुज
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - बहुविकल्पी प्रश्न7videos
त्रिकोणमिति के कुछ अनुप्रयोग
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - लघु उत्तरात्मक प्रश्न21videos
दो चर वाले रैखिक समीकरण युग्म
Similar Questions
मान लीजिए ΔABC~ΔDEF है और इनके क्षेत्रफल क्रमशः 64cm2 और 121cm2 हैं । यदि EF = 15.4 cm हो , तो BC ज्ञात कीजिए ।
08:08View Solutionकुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं । निर्धारित कीजिए कि इनमें से कौन - कौन से त्रिभुज समकोण विभुज हैं । इस स्थिति में कर्ण की लंबाई भी लिखिए ।
( i ) 7 cm , 24 cm , 25 cm
( ii ) 3 cm , 8 cm , 6 cm
( iii ) 50 cm , 80 cm , 100 cm
( iv ) 13 cm , 12 cm , 5 cm .07:14View Solutionआकृति (i) और (ii) में DE||BC है | ज्ञात कीजिए |
(i) में, EC और (ii) में AD ज्ञात कीजिए: (i)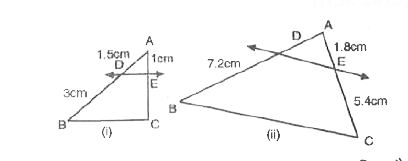
07:01View Solutionपहाड़ी के शिखर से उसके पाद के 40 किमी दूरी का अवनमन कोण 45∘ है । पहाड़ी की ऊँचाई होगी :
( A ) 30 किमी ( B ) 35 किमी
( C ) 40 किमी ( D ) 45 किमी ।04:57View Solutionनिम्न रैखिक समीकरण के युग्म को हल कीजिए ।
2x+3y=13
5x−4y=−206:28View SolutionCD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिन्दु D और H क्रमशः ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं । यदि ΔABC~ΔFEG तो दर्शाइए कि
(i) CDGH=ACFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF04:55View SolutionCD and GH are the bisectors of ∠ACB and ∠EGF respectively. If D lies on AB of ΔABC and H lies on EF of ΔEFG and if ΔABC~ΔEFG, then prove that (a) CDGH=ACFG, (b)ΔDCB~ΔHGE, (c)ΔDCA~ΔHGF
04:23View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
CDGH=ACFG04:23View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCB~ΔHGE07:39View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCA~ΔHGF03:34View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
CDGH=ACFG07:41View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCB~ΔHGE03:43View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCA~De<HGF04:27View Solutionसदिशों के प्रयोग द्वार सिद्ध कीजिए कि बिंदु A(−2,3,5),B(7,0,−1),C(−3,−2,−5) और D(3,4,7) इस प्रकार हैं कि AB और CD बिंदु P(1,2,3) पर प्रतिच्छेद करते हैं।
03:30View Solutionयदि A और B दो वर्ग आव्यूह इस प्रकार हैं कि AB = A और BA = B तो सिद्ध करो कि A और B समशम होंगे |
View SolutionCD and GH are respectively the bisectors of ⌊ACBand⌊EGF such that D and H lie on sidea AB and FE of ΔABCandΔEFG respectively. If ΔABC~ΔFEG, show that.
i] CDGH=ACFG
ii] ΔCDB~ΔHGE
iii] ΔDCA~ΔHGFView Solution