Construct a triangle XYZ in which XY=8 cm , the median XA drawn from X to YZ is 6.6 cm and the median YB drawn from Y to XY is 7.2 cm.
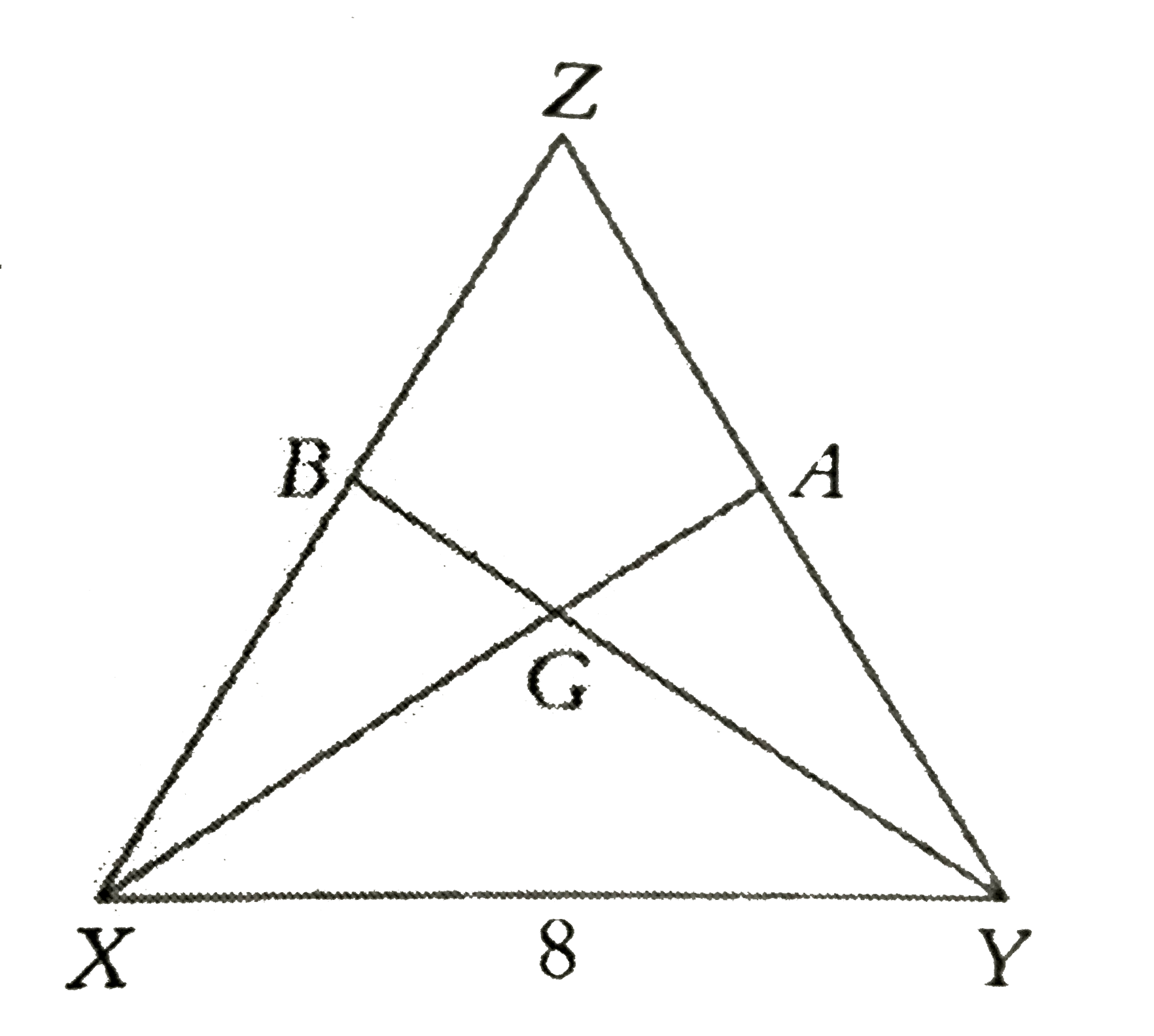
We know that the centroid (G) divides a median in the ratio 2:1 from the vertex.
∴XG=4.4 cm and GA=2.2 cm (∵XA=6.6cm)
YG=4.8mc and GB=2.4cm (∵YB=7.2cm)
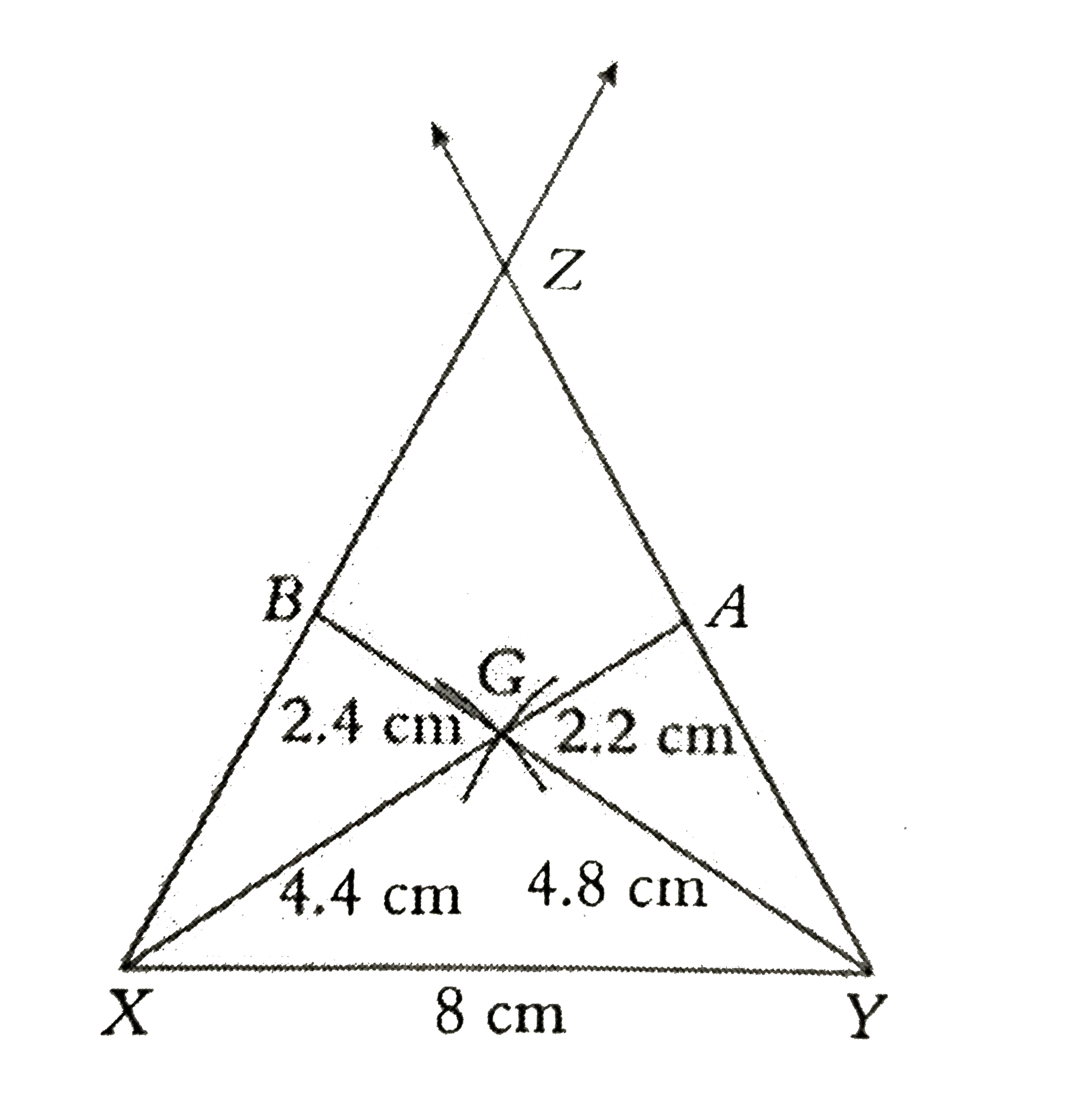
(a) Draw a line segment XY=8 cm.
(b) With X as the centre and 4.4 cm as radius draw an arc.
(c ) With Y as the centre and 4.8 cm as radius draw another arc to cut the previous arc at G.
(d) Produce XG to the point A such that AG=2.2 cm.
(e ) Produce YG to the point B such that GB=2.4 cm.
(f) Join XB and YA and produce them to meet at Z. Now XYZ is required triangle.
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - very short answer type question
25 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Short Answer Type Questions 31
9 Videos
- FormulaeBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 3
7 Videos
- INDICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)
7 Videos
Similar Questions
Knowledge Check
The following sentences are the steps involved in construction of the incircle for the triangle XYZ in which ∠Y=90∘,XZ=6 cm and YZ=4 cm.
Arrange them in sequential order from the first to the last.
(A) Mark the foot of the perpendicular from I onto YZ as D.
(B) Construct the triangle XYZ with ∠Y=90∘,XZ=6 cm and YZ=4cm.
(C ) Draw a circle with I as the centre and ID as radius. This is the required incircle.
(D) Draw the bisectors of ∠X,∠Y and ∠Z and mark their point of concurrence as I.ABDCABDBACCDBCADBDACABC is a right isosceles triangle with ∠B=90∘. If length of median from B to AC is 6 cm then area of triangle is
A9cm2B72cm2C36cm2D18cm2
Construct a ΔABC in which AB=4.5 cm, BC=6 cm and median AD=4 cm.
View SolutionConstruct a triange ABC in which AD,BE and CF are the medians with AD=5.4cm,BE=6 cm and CF=8.1cm.
View SolutionConstruct a triangle ABC in which AB = 5 cm, BC = 6-8 cm and median AD = 4.4 cm. Draw incircle of this triangle.
View SolutionConstruct the incircle for the triangle XYZ in which ∠Y=90∘,XZ=4.5cmandYZ=3cm
View SolutionConstruct a triangle XYZ where ∠X=60∘,∠Y=40∘, and XY = 5 cm.
View SolutionThe following sentences are the steps involved in construction of the incircle for the triangle XYZ in which ∠Y=90∘,XZ=6 cm and YZ=4 cm.
Arrange them in sequential order from the first to the last.
(A) Mark the foot of the perpendicular from I onto YZ as D.
(B) Construct the triangle XYZ with ∠Y=90∘,XZ=6 cm and YZ=4cm.
(C ) Draw a circle with I as the centre and ID as radius. This is the required incircle.
(D) Draw the bisectors of ∠X,∠Y and ∠Z and mark their point of concurrence as I.
View Solution
