String going over a pulley connects two blocks of masses m, and my. String and pulley are light. Calculate acceleration of centre of mass of blocks system.

We can apply Newton.s laws of motion to find acceleration of blocks. Let me is moving down with acceleration a then my must be moving up with the same acceleration. Acceleration can be written as follows:
a=(m2−m1m1+m2)g
Let us assume downward direction as the positive direction then acceleration of centre of mass of blocks can be written as follows:
acm=m2a−m1am1+m2=(m2−m1m1+m2)a
Substituting value of a, we can write as follows:
acm=(m2−m1m1+m2)×(m2−m1m1+m2)g
⇒acm=(m2−m1m1+m2)2g
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - REVISION EXERCISES (Very Short Answer Questions Carrying 1 mark)
29 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - REVISION EXERCISES (Additional Questions Carrying 1 mark )
4 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE (NCERT EXEMPLAR PROBLEMS (SUBJECTIVES QUESTIONS) (Very Short Answer Type Questions))
9 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View Solution
Knowledge Check
A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of masses is
A8:1B4:3C5:3D9:7A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
A(a) 8:1B(b) 9:7C(c) 4:3D(d) 5:3A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
A8:1B9:7C4:3D5:3
Two blocks are resting on ground with masses 5 kg and 7 kg. A string connected them which goes over a massless pulley A. There is no friction between pulley and string A. Find acceleration of centre of mass of the system of two masses (in m/s2
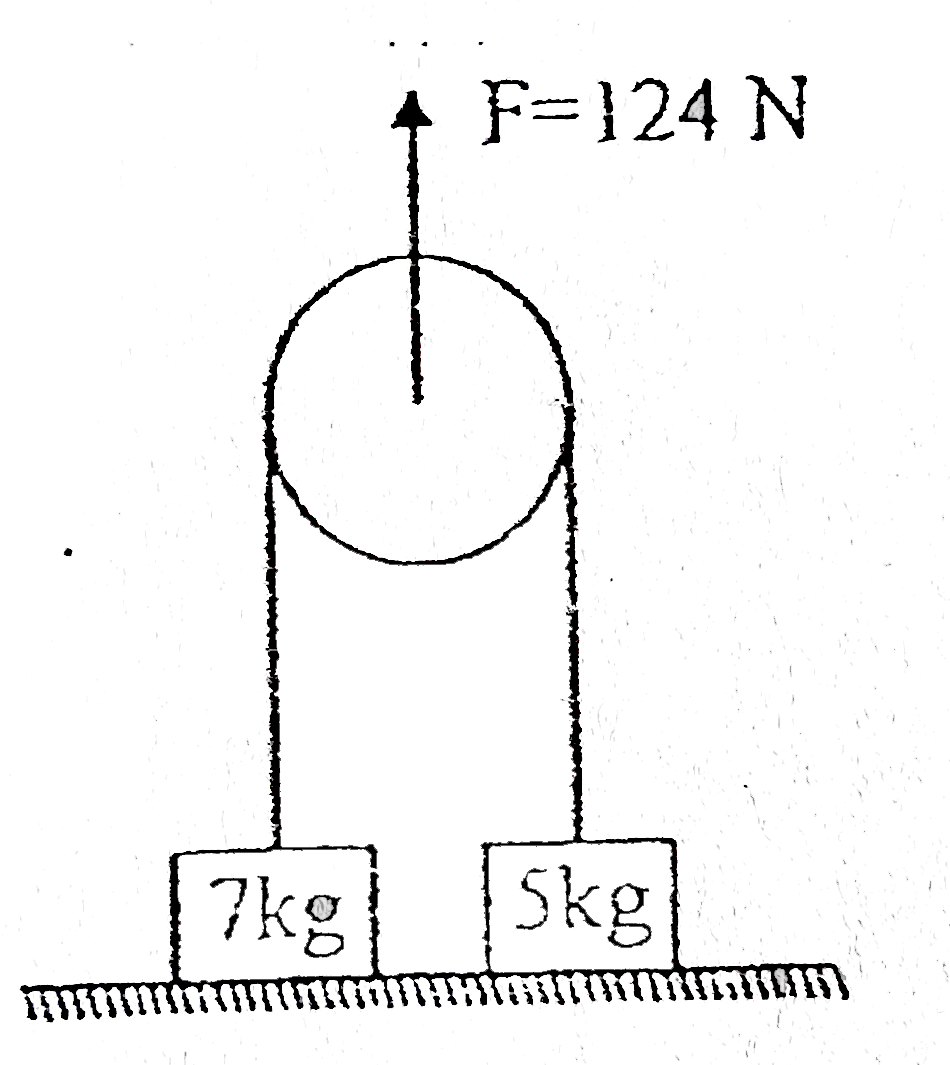
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
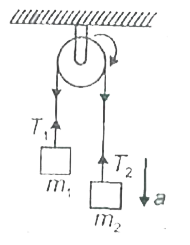
View SolutionFigure shows a pulley of mass m and radius r with two blocks of masses m1 and m2 attached with a light and unstretchable string. Find the acceleration of the blocks, tensions in the string and the force exerted by the pulley on the celling from which it is hanging. Assume no slipping between the string and the wheel.
View SolutionTwo blocks are resting on ground with masses 5 kg and 7 kg. A spring connected them which goes over a massless pulley A. There is no friction between pulley and string A. Find acceleration of centre of mass of the system of two masses (in m/s2
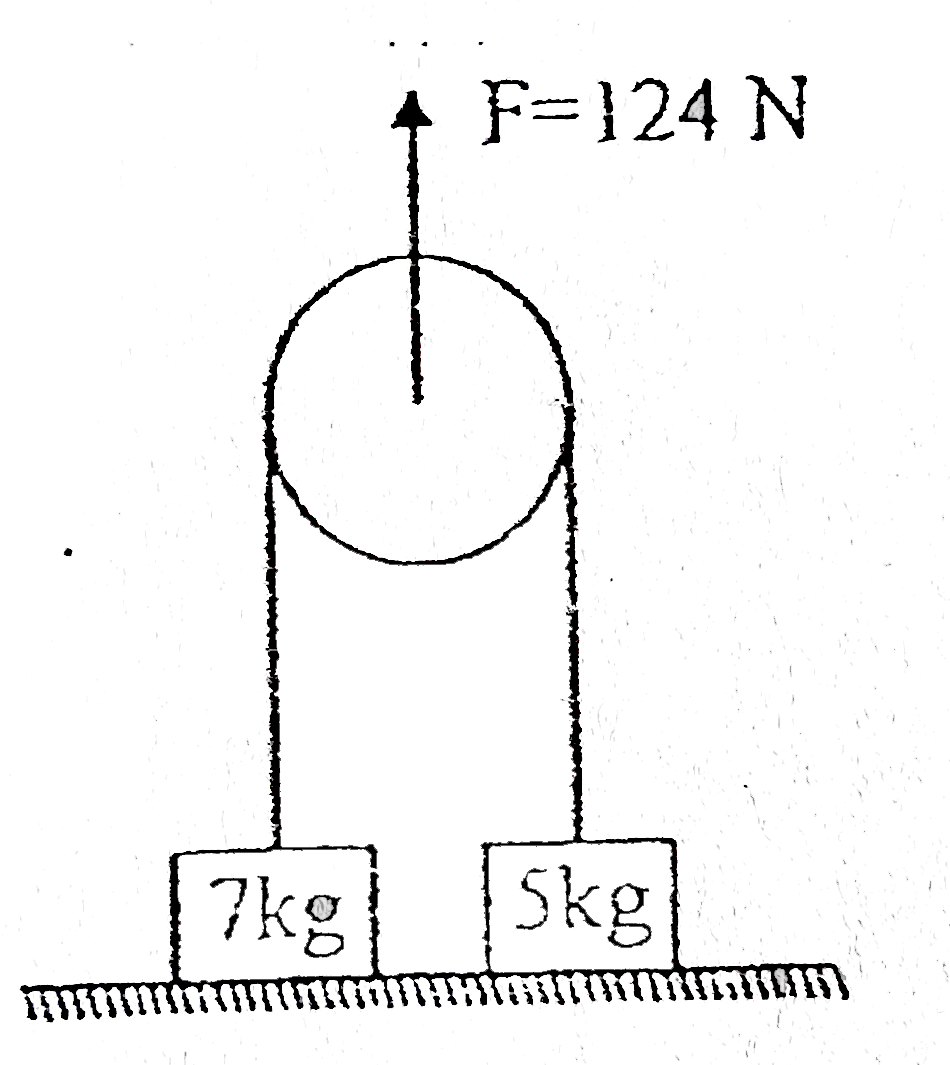
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View Solution
