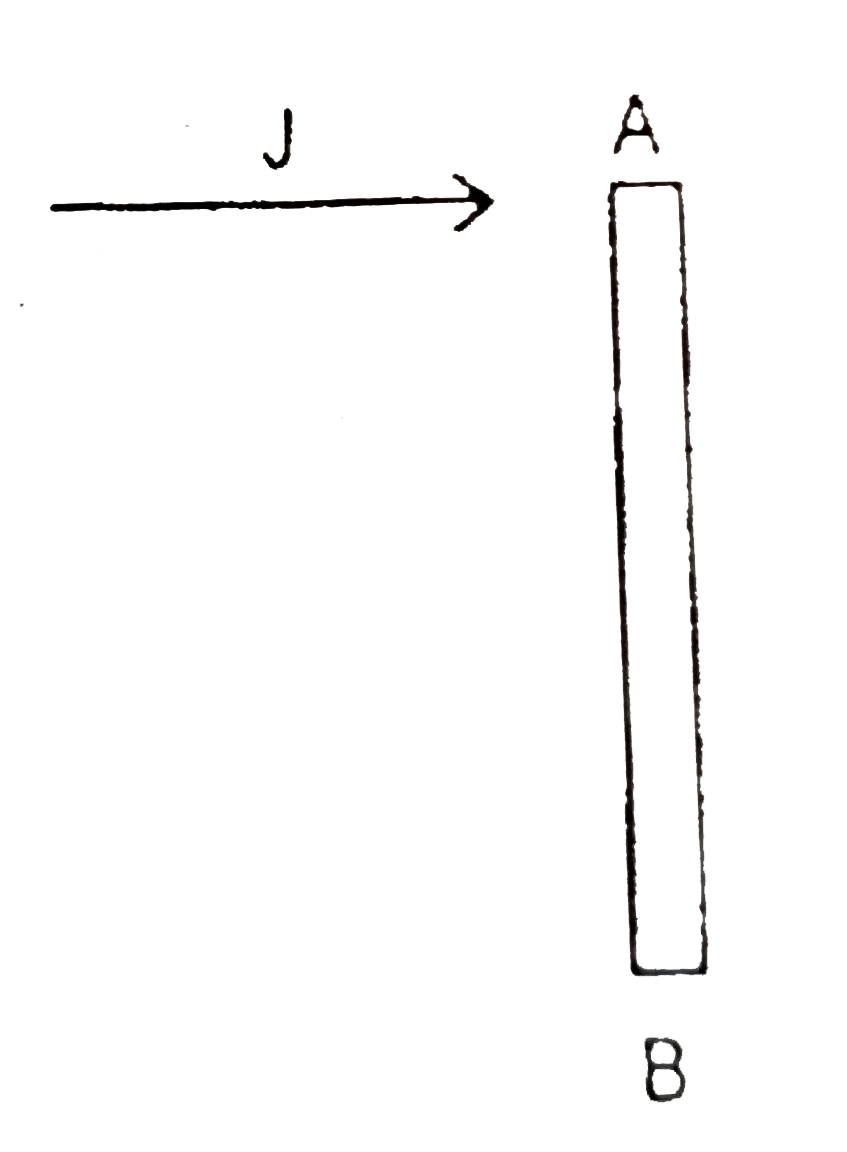
A uniform rod of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to end B as shown.

Distance travelled by the centre of the rod, while rod rotates by $90^{\circ}$

Video Solution

Text Solution

Verified by Experts

Let force Facts at the end of the rod for a very brief period $Δ t$ and as a result centre of mass of rod acquires velocity v and angular velocity about its centre of mass. Linear impulse - change in linear momentum $\Rightarrow F Δ t = m v \Rightarrow v = \frac{F Δ t}{m} ... (1)$
In above equation mis mass of the rod. Angular impulse about the centre - Angular momentum of rod about the centre.
$\Rightarrow F \frac{L}{2} Δ t = I ω$
$\Rightarrow F \frac{L}{2} Δ t = \frac{M L^{2}}{12} ω \Rightarrow ω = \frac{6 F Δ}{m L} ... (2)$
Distance travelled by the centre of the rod by the time it rotates through an angle $π / 2$ can be written as follows:
$x = v \times \frac{π}{2 ω}$
Substituting values from equations (1) and (2) we get the following:
$x = \frac{F Δ t}{m} \times \frac{π}{2 \frac{6 F Δ t}{m L}} = \frac{π L}{12}$

Updated on:21/07/2023

A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
A $(2 π \frac{m l}{p}$
B $(2 π) (\frac{p}{m l}$
C $\frac{π m l}{12 p}$
D $\frac{π p}{m l}$
A uniform rod $A B$ of mass $m$ and length $l$ at rest on a smooth horizontal surface. An impulse $P$ is applied to the end $B$ . The time taken by the rod to turn through a right angle is $:$

A $\frac{2 π m l}{P}$
B $\frac{π m l}{3 P}$
C $\frac{π m l}{12 P}$
D $\frac{2 π m l}{3 P}$
A uniform rod $A B$ of mass $m$ and length $l$ at rest on a smooth horizontal surface . An impulse $P$ is applied to the end $B$ . The time taken by the rod to turn through a right angle is $:$

A $\frac{2 π m l}{P}$
B $\frac{π m l}{3 P}$
C $\frac{π m l}{12 P}$
D $\frac{2 π m l}{3 P}$