A hoop of radius r and mass m rotating with an angular velocity $ω_{0}$ is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip?

A

$\frac{r ω_{0}}{3}$

B

$\frac{r ω_{0}}{2}$

C

$r ω_{0}$

D

$\frac{r ω_{0}}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

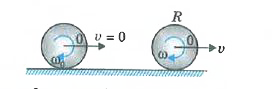
Using law of conservation of angular momentum about point of contact.
$L_{1} = m r^{2} ω_{0}$
$L_{2} = m r^{2} (\frac{v}{r}) + m v r = 2 m v r$
$L_{1} = L_{2} \Rightarrow v = \frac{r ω_{0}}{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A hoop of radius $r$ mass $m$ rotating with an angular velocity $ω_{0}$ is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
A $\frac{r ω_{0}}{2}$
B $r ω_{0}$
C $\frac{r ω_{0}}{4}$
D $\frac{r ω_{0}}{3}$
Question 2 - Select One
A solid sphere with a velocity (of centre of mass) $v$ and angular velocity $ω$ is gently placed on a rough horizontal surface. The frictional force on the sphere :
Amust be forward (in direction of $v$ )
Bmust be backward (opposite to $v$ )
Ccannot be zero
Dnone of the above
Question 3 - Select One or More
A disc is given an initial angular velocity $ω_{0}$ and placed on a rough horizontal surface as shown Fig. The quantities which will not depend on the coefficient of friction is/are

Athe time until rolling begins
Bthe displacement of the disc until rolling begins
Cthe velocity when rolling begins
Dthe work done by the force of friction

MODERN PUBLICATION-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )

Home
Ask Doubt
Profile