A current carrying wire heats a metal rod. The wire provides a constant power P to the rod. The metal rod is enclosed in an insulated container. It is observed that the temperature (T) in the metal rod change with the (t) as T(t)=T0(1+βt1/4) where β is a constant with appropriate dimension of temperature. the heat capacity of metal is :
4P(T(t)−T0)3β4T40
4P(T(t)−T0)β4T20
4P(T(t)−T0)4β4T50
4P(T(t)−T0)4β4T30
The correct Answer is:A
4P(T(t)−T0)3β4T40
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTION ((C ) MULTIPLE CHOICE QUESTION WITH MORE THAN ONE CORRECT ANSWER)
11 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTION ((D ) MULTIPLE CHOICE QUESTION BASED ON A GIVEN PASSAGE/COMPREHENSION )
9 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION FROM CPMPETITIVE EXAMINATION ) JEE MAIN AND OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)
19 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Chapter Practice Test (for Board Examination)
16 Videos
- UNITS AND MEASUREMENTBOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A metal rod is placed along the axis of a solenoid carrying a high-frequency alternating current. It is found that the rod gets heated. Explain why the rod gets heated .
View SolutionOne end of a rod, enclosed in a thermally insulating sheath, is kept at a temperature T1 while the other, at T2. The rod is composed of two sections whose lengths are l1 and 12 and heat conductivity coefficients x1 and x2. Find the temperature of the interface.
View Solution
Knowledge Check
A thermally isulated piece of metal is heated under atmospheric pressure by an electric current so that it receives electric energy at a constant power P. This leads to an increase of absolute temperature T of the metal with time t as follows:
T(t)=T0[1+a(t−t0)]1/4. Here, a, t0 and T0 are constants. The heat capacity Cp(T) of the metal isA4PaT0B4PTaT40C2PTaT40D2PaT0If a piece of metal is heated to temperature θ and the allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closet to
A B
B C
C D
D
The current in a metallic conductor is plotted against voltage at two different temperatures T1 and T2. Which is correct
 AT1>T2BT1<T2CT1=T2Dnone
AT1>T2BT1<T2CT1=T2Dnone
The specific heat of a metal at low temperatures varies according to S=(45)T3, where T is the absolute temperature, Find the heat energy (in SI unit) needed to rate the temperature of unit mass of the metal from T=1K to T=2K
View SolutionA cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T0 and the furnace is maintained at T1=T0+ΔT1. The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T2=T0+ΔT2[ΔT2<<T0]. The exposed surface of the rod has emissivity e. Prove that ΔT1 is proportional to ΔT2 and find the proportionality constant.
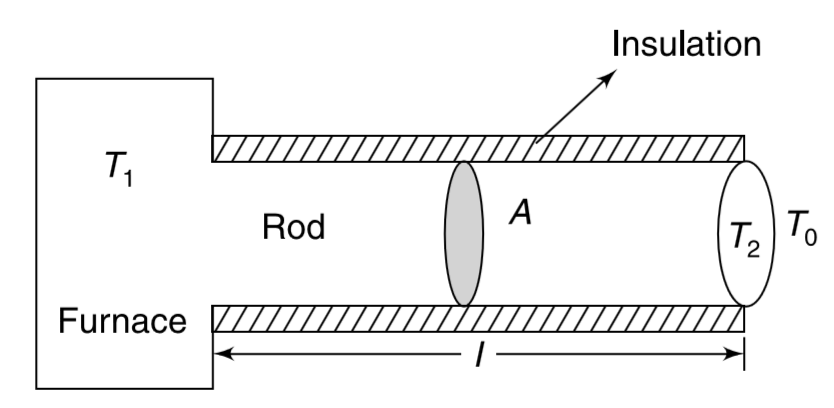
View SolutionA thermally insulated piece of metal is heated under atmosphere by an electric current so that it receives electric energy at a constant power P. This leads to an increase of the absoulute temperature T of the metal with time t as follows T=a14. then the heat capacity Cp is
View SolutionThe amount of heat energy radiated by a metal at temperature T is E. When the temperature is increased to 3T, energy radiated is
View Solution
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will be
View Solution