A Gaussian surface in the fig. is shown by dotted line. The electric field on the surface will be :-

due to q1 and q2 only
due to q2 only
zero
due to all
The correct Answer is:D
We should know that electric field intensity on the Gaussian surface is taken due to all the charges, inside or outside the closed surfacc. But surface integral of electric field over the three-dimensional closed surface depends only on the enclosed charges.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (C.MCQ))
19 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (D.MCQ) Passage )
10 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BB.MCQ))
22 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
A spherical Gaussian surface encloses, and is concentric with, a charged spherical conductor. If the TNEI over the Gaussian surface is negative, what can you say about the electric field →E at a point on the surface?
View SolutionA point charge of 2.0μC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
View Solution
Knowledge Check
A Gausisan surface in the figure is shown by dotted line.
The electric field on the surface will be
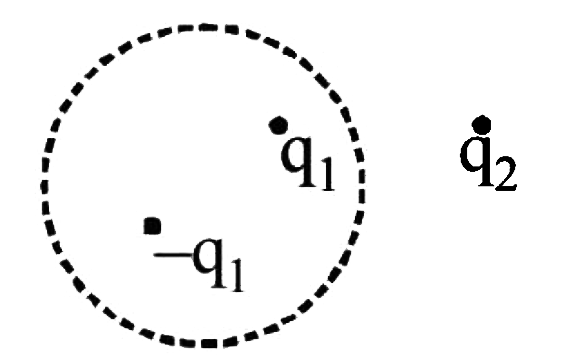 A(a) due to q1 and q2 onlyB(b) due to q2 onlyC(c) zeroD(d) due to all
A(a) due to q1 and q2 onlyB(b) due to q2 onlyC(c) zeroD(d) due to allA Gaussian surface encloses a proton p. The electric field at any point on the surface is →€. The flux linked with the Gaussian surface is ϕ.
STATEMENT-1 : When an electron is kept close to this system outside the Gaussian surface, the flux linked with the surface would change.
and
STATEMENT-2 : The presence of electron will alterthe electric field on the gaussian surface.AStatement-1 is True, Statement-2 is True, Statement -2 is a correct explanation for Statement-1BStatement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1CStatement-1 is True, Statement -2 is FalseDStatement-1 is False, Statement-2 is True.S1: When a positively charged particle is released in an electric field , in its subsequent motion,it may or may not move along the electric field line passing through the point it has been released.
S2: In electrostatic, conductors are always equipotential surfaces.
S3: The flux through a closed Gaussian surface is non-zero. The electric field at some point on the Gaussian surface may be zero.ATTFBFTFCTTTDFFF
A point charges of 2.0μC is at the centre of a cubic Gaussian surface 9.0cm on edge . What is the net electric flux through the surface?
View SolutionIf the flux of the electric field through a closed surface is zero,
View SolutionIf the net electric field flux passing through a closed surface is zero, then the electric field at the surface will be
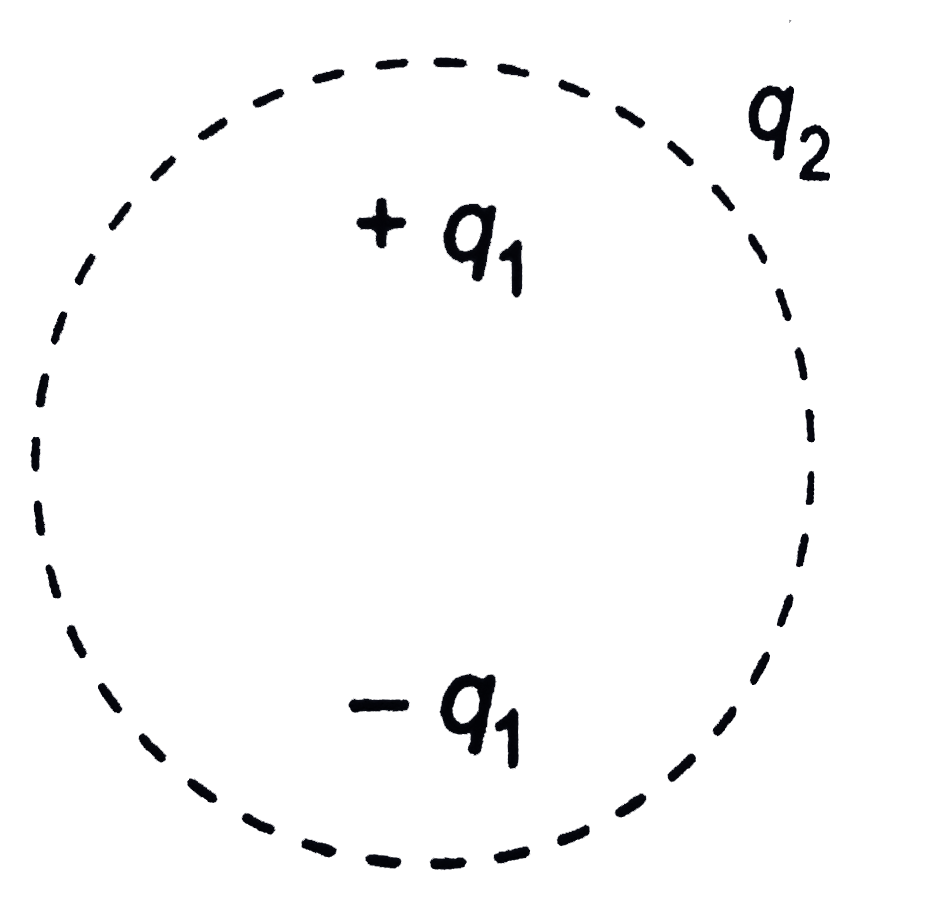
View SolutionConsider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.
View SolutionA point charge of 1.77 μC is at the centre of a cubical gaussian surface having each side 50 cm. what is the net electric flux through the surface?
View Solution
