Three concentric metallic spherical shells of radii R, 2R, 3R, are given charges Q1, Q2, Q3, respectively. It is found that the surface charge denisties on the outer surfaces of the shells are equal. Then, the ratio of the charges given to the shells, Q1:Q2:Q3, is
1:2:3
1:3:5
1:4:9
1:8:18
The correct Answer is:B
Simple rules for solving this question.
 One is that metal surfaces facing each other must always carry equal and opposite charge and the other rule is that net charge of an isolaled object remains constant.
One is that metal surfaces facing each other must always carry equal and opposite charge and the other rule is that net charge of an isolaled object remains constant.
Net charge with each spherical shell is given. See how the charge is distributed. Surface charge densities on required surfaces can be written as follows:
σ1=Q14πR2….(i)
σ2=Q1+Q24π(2R)2⇒σ2=Q1+Q216πR2 …(ii)
σ3=Q1+Q2+Q34π(3R)2=σ3=Q1+Q2+Q336πR2…(iii)
σ1=σ2
σ1=σ2⇒Q14πR2=Q1+Q216πR2
⇒4Q1=Q1+Q2⇒3Q1=Q2...(iv)
σ2=σ3⇒Q1+Q216πR2=Q1+Q2+Q336πR2
⇒9Q1+9Q2=4Q1+4Q2+4Q3
⇒5Q1+5Q2=4Q3
Substituting Q2 from equation (iv) in terms of Q1 we get the following :
⇒5Q1+15Q1=4Q3
⇒Q3=5Q1...(v)
From equation (iv) and (v) we can write the following :
Q1:Q2:Q3=1:3:5
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (C.MCQ))19videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (D.MCQ) Passage )10videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BB.MCQ))22videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST15videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION14videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Concentric metallic hollow spheres of radii R and 4R hold charges Q1andQ2 respectively. Given that surface charge densities of the concentric spheres are equal, the potential difference V(R)−V(4R) is :
View SolutionThere are two concentric metallic shells of radii R and 2R, if outer shell is given charge q1 , then charge on surface of inner shell will be
View Solution
Knowledge Check
- Question 1 - Select One
Three concentric metallic spherical shells of radii R, 2R, 3R are given charges Q1Q2Q3, respectively. It is found that the surface charge densities on the outer surface of the shells are equal. Then, the ratio of the charges given to the shells Q1:Q2:Q3 is
A1:2:3B1:3:5C1:4:9D1:8:18 - Question 2 - Select One
Three concentric metallic spherical shells of radii R, 2R, 3R are given charges Q1Q2Q3, respectively. It is found that the surface charge densities on the outer surface of the shells are equal. Then, the ratio of the charges given to the shells Q1:Q2:Q3 is
A1:2:3B1:3:5C1:4:9D1:8:18 - Question 3 - Select One
Two concentric spherical shells of radii R and 2R are given charges Q1andQ2 respectively.
The surfaces charge densities of the outer surfaces are equal. Determine the ratio Q1:Q2.A1:2B4:1C1:4D2:1
Two conducting hollow spherical shells of radius R and 2R carry charges -Q and 3Q respectively. How much charge will flow into the earth if inner shell is grounded?
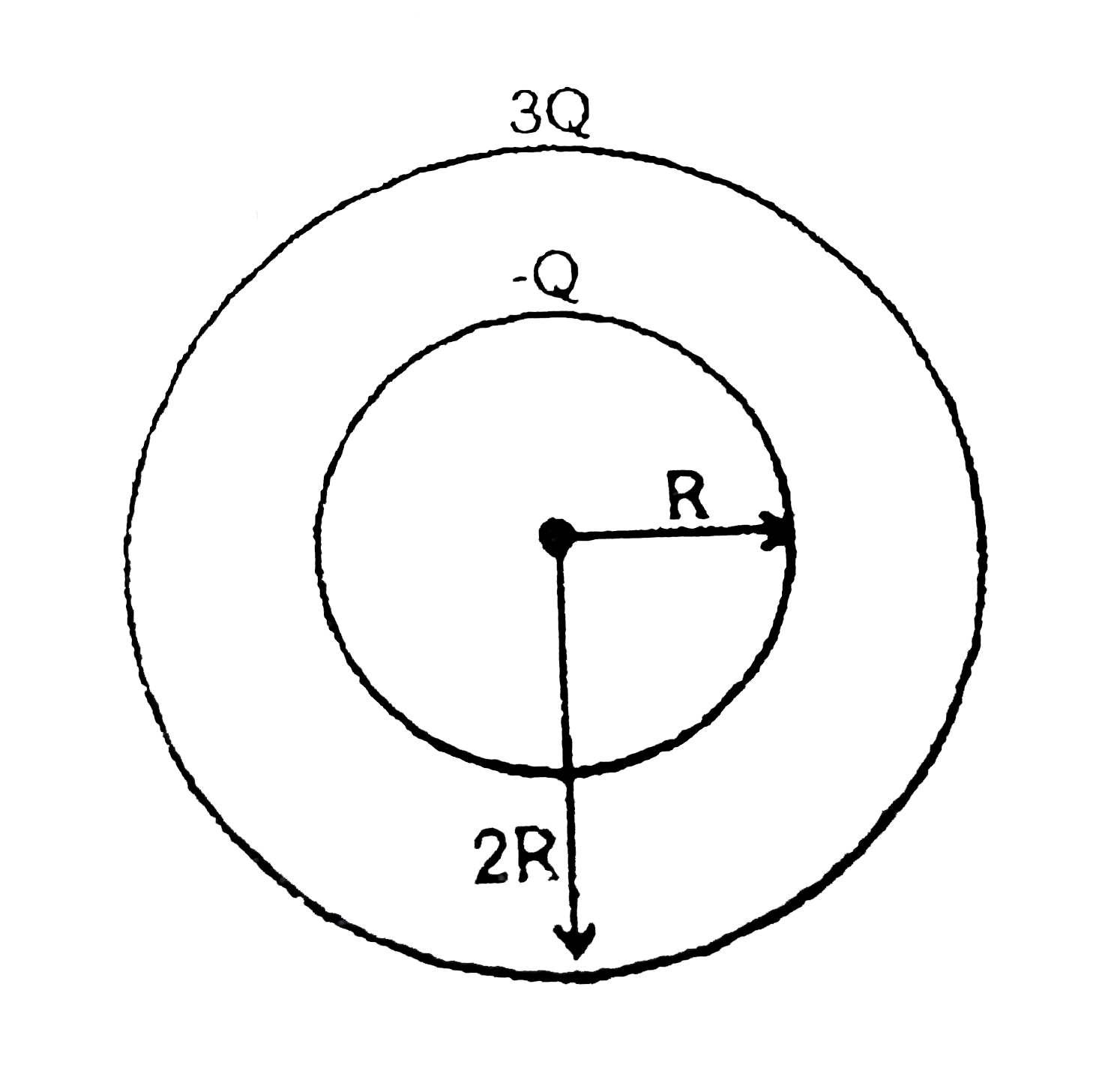 View Solution
View SolutionTwo uniformly charged concentric spherical shells of radius R and r, are given charges Q1 and Q2 respectively. If their potential difference is V, then it will not depends upon:
 View Solution
View SolutionThree concentric conducting spherical shells have radii r, 2r, and 3r and charges q1,q2andq3, respectively. Innermost and outermost shells are earthed as shown in figure. The charges shown are after earthing. Select the correct alternative.
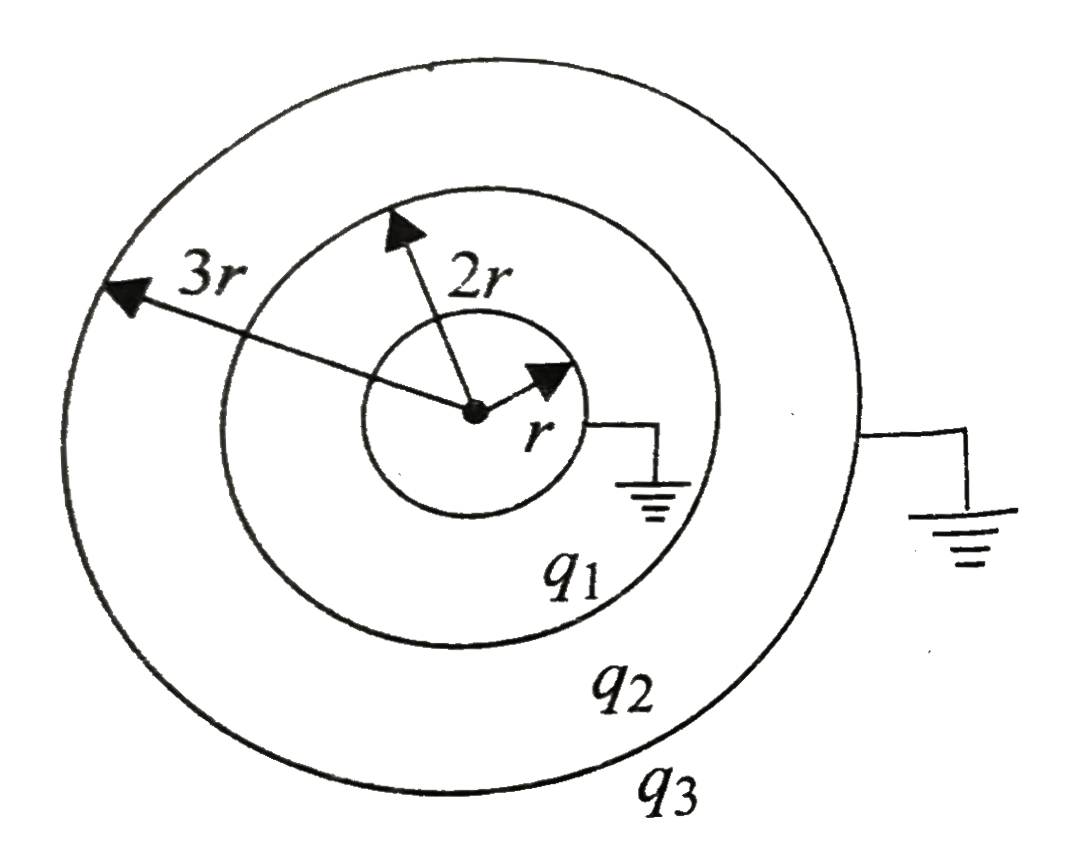 View Solution
View SolutionThere are three concentric metallic spherical shells of radii R, 2R and 3q, respectively. The middle spherical shell is connected to earth. Let q1 be the charge appearing on the inner surface of the middle sphere and q2 be the charge on outer surface of the middle sphere. Similarly q3 is the charge appearing on inner surface of outermost sphere and q4 is the charge appearing on outer surface of outermost sphere.
 View Solution
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View Solution
