There are three concentric metallic spherical shells of radii R, 2R and 3q, respectively. The middle spherical shell is connected to earth. Let q1 be the charge appearing on the inner surface of the middle sphere and q2 be the charge on outer surface of the middle sphere. Similarly q3 is the charge appearing on inner surface of outermost sphere and q4 is the charge appearing on outer surface of outermost sphere.

PQRS4312
PQRS4321
PQRS3412
PQRS3421
The correct Answer is:A
The middle sphere is earthed hence the answers are not affected by the amount of charge given on this sphere because it will gain such a charge from earth that its electric potential becomes zero.
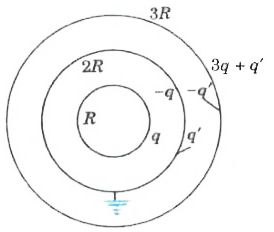
Since electric field intensity inside the innermost sphere is zero so no charge can stay on the inner surface and all charge q of inner sphere will stay on its outer surface only as shown in the figure. Metal faces parallel to each other must carry equal and opposite charges and hence charge appearing on inner surface of middle sphere must be -q. Let charge on outer surface of middle sphere be q. so that its electric potential may become zero. We shall calculate q. later by equating potential of middle sphere to zero. For now charge -q. must appear on inner surface of the outermost sphere, which is isolated. Hence, the net charge on it must remain 3q and hence the charge on outer surface must be 3q+q..
Now we can calculate the value of q. by equating potential of middle sphere equal to zero because this sphere is connected to earth and the conductor connected to earth always acquire zero potential.
Vmiddle-sphere=14πε0[q2R+q.−q2R+3q3R]
Note that we have used only the net charge on spheres to calculate potential of the middle sphere. We know that middle sphere is earthed hence:
Vmiddle-sphere=14πε0[q2R+q.−q2R+3q3R]=0⇒q.=−2q
Now we can write the charges appearing on different faces:
q1=−q
q2=−2q
q3=2q
q4=q
We can see that option (a) is correct.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Competition file (MATRIX TYPE QUESTIONS)
1 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Competition file (INTEGER TYPE QUESTIONS)
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Competition file (ASSERTION REASON TYPE QUESTIONS)
8 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
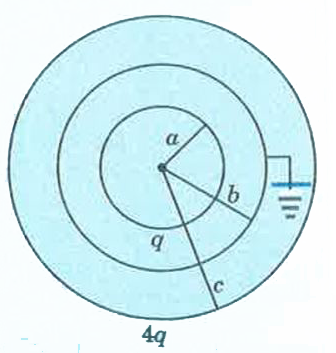
There are three concentric metallic spherical shells of radius a, b and c respectively as shown in the figure. The innermost sphere is given a charge q and the outermost sphere is given a charge 4q while the middle sphere is earthed. Find the charges appearing on the inner and outer surfaces of middle sphere.
View SolutionThere are three concentric metallic spherical shells of radius R, 2R and 3R. Charge Q is given to the innermost spherical shell. If the innermost spherical shell is connected with a metal wire to the outermost spherical shell without touching the middle shell, which is connected to the earth, then, find charges appearing on all surfaces.
View Solution
Knowledge Check
Three concentric conducting spherical shells carry charges as : +4Q on the inner shell, −2Q on the middle shell and −5Q on the outer shell. The charge on the inner surface of the outer shell is
A0B4QC−QD−2QThree concentric metallic spherical shells of radii R, 2R, 3R, are given charges Q1, Q2, Q3, respectively. It is found that the surface charge denisties on the outer surfaces of the shells are equal. Then, the ratio of the charges given to the shells, Q1:Q2:Q3, is
A(a) 1:2:3B(b) 1:3:5C(c) 1:4:9D(d) 1:8:18Three concentric metallic spherical shells of radii R, 2R, 3R are given charges Q1Q2Q3, respectively. It is found that the surface charge densities on the outer surface of the shells are equal. Then, the ratio of the charges given to the shells Q1:Q2:Q3 is
A1:2:3B1:3:5C1:4:9D1:8:18
Three concentric conducting spherical shells carry charges as : +4Q on the inner shell, −2Q on the middle shell and −5Q on the outer shell. The charge on the inner surface of the outer shell is
View SolutionFigure shows three concentric metallic spherical shells. The outermost shell has charge q2, the inner most shell has charge q1, and the middle shell is uncharged. The charge appearing on the inner surface of outermost shell is
View SolutionThere are two concentric metallic shells of radii R and 2R, if outer shell is given charge q1 , then charge on surface of inner shell will be
View SolutionThree concentric metallic spherical shells of radii R, 2R, 3R are given charges Q1Q2Q3, respectively. It is found that the surface charge densities on the outer surface of the shells are equal. Then, the ratio of the charges given to the shells Q1:Q2:Q3 is
View SolutionThree concentric conducting sphereical shells carry charges +4Q on the inner shell −2Q on the middle shel and +6Q on the outer shell. The charge on the inner surface of the outer shell is
View Solution
