In the figure given below there is one parallel plate capacitor with two types of dielectric materials in between the plates. Calculate net capacitance of the given system.

Text Solution

Verified by Experts

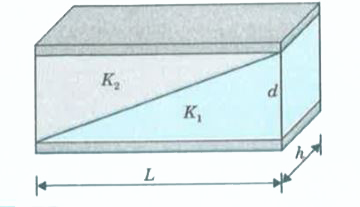
We can see that thickness of each dielectric material between the plates is continuously changing as we move from one end to the other and we need to apply math of intergration to get the capacitance of the system.

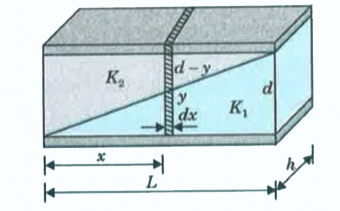
Let us select a segment of width dx at a distance x from the left end of the capacitor as shown in the figure. Let y represent thickness of dielectric material with dielectric constant $K_{1}$ for this capacitor segment and d-y the thickness of dielectric material with dielectric constant $K_{2}$ . We can easily understand that capacitor segment can be further divided in two segments $d C_{1}$ and $d C_{2}$ connected is series with each other to represent the complete capacitor segment as shown in the figure.

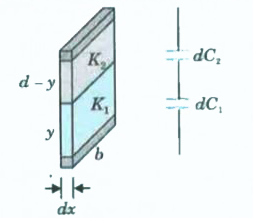
Let dC be the capacitance of selected capacitor segment then we can write the following:
$\frac{1}{d C} = \frac{1}{d C_{1}} + \frac{1}{d C_{2}} ... (i)$
further we can write:
$d C_{1} = \frac{K_{1} ε_{0} (b d x)}{y} & d C_{2} = \frac{K_{2} ε_{0} (b d x)}{d - y} ... (i i)$
Substituting the valuco of $d C_{1} and d C_{2}$ from equation (ii) in equation (i) we get the following:
$\frac{1}{d C} = \frac{y}{K_{1} ε_{0} (b d x)} + \frac{d - y}{K_{2} ε_{0} (b d x)}$
$\Rightarrow \frac{1}{d C} = \frac{K_{2} y + K_{1} (d - y)}{K_{1} K_{2} ε_{0} (b d x)} = \frac{K_{1} d + (K_{2} - K_{1}) y}{K_{1} K_{2} ε_{0} (b d x)}$
$\Rightarrow d C = \frac{K_{1} K_{2} ε_{0} (b d x)}{K_{1} d + (K_{2} - K_{1}) y} ... (i i i)$
All capacitor segments are supposed to be connected in parallel to each other so we can integrate dC in equation (iii) to get the overall capacitance of this system. But before we can actually integrate equation (iii), we first need to decide on the variable of integration. Is it x or y? Both are related to each other but using geometry we can wirte the following equation:
$\frac{d}{L} = \frac{y}{x} \Rightarrow d x = \frac{L}{d} d y ... (i v)$
We can substitue dx in terms of dy from equation (iv) into equation (iii) to get the following equation.
$d C = \frac{K_{1} K_{2} ε_{0} b L}{d} (\frac{d y}{K_{1} d + (K_{2} - K_{1}) y}) ... (v)$
We can understand that variable y changes from zero to d as x changes from 0 to L. Now using suitable limits of integration we can integrate equation (v) to get the net capacitance of this system.
$C = \frac{K_{1} K_{2} ε_{0} b L}{d} \int_{y = 0}^{y = d} \frac{d y}{K_{1} d + (K_{2} - K_{1}) y}$
$\Rightarrow C = \frac{K_{1} K_{2} ε_{0} b L}{d} {[\frac{1}{K_{2} - K_{1}} ln {K_{1} d + (K_{2} + K_{1}) y}]}_{0}^{d}$
$\Rightarrow C = \frac{K_{1} K_{2} ε_{0} b L}{d (K_{2} - K_{1}) ln \frac{K_{2}}{K_{1}}}$

Updated on:21/07/2023

A parallel plate capacitor is filled with dielectrics. What is capacitance?

A $\frac{2 K_{1} K_{2}}{K_{1} + K_{2}}$
B $\frac{K_{1} K_{2}}{K_{1} + K_{2}}$
C $\frac{2 ε_{0} A}{d} (\frac{K_{1} K_{2}}{K_{1} + K_{2}})$
D $\frac{2 ε_{0} A}{d} (\frac{2 K_{1} + K_{2}}{2 K_{1} K_{2}})$
A parallel plate capacitor with air between plates (dielectric constant K =2) has a capacitance C. If the air is removed, then capacitance of the capacitor is
A $\frac{C}{\sqrt{2}}$
B $\frac{C}{2}$
C $\sqrt{2} C$
D2C
A dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
Abecomes zero
Bremains the same
Cdecreases
Dincreases