Twelve identical capacitors of capacitance C are connected across each edge of a cube. Find equivalent capacitance across one of the face diagonals.
To find the equivalent capacitance across one of the face diagonals of a cube formed by 12 identical capacitors of capacitance C, we can follow these steps:
Step 1: Understand the Configuration
We have a cube where each edge has a capacitor of capacitance C. We need to find the equivalent capacitance across one of the face diagonals, say from point A to point C.
Step 2: Visualize the Cube
Label the vertices of the cube as follows:
- A (front bottom left)
- B (front bottom right)
- C (front top right)
- D (front top left)
- E (back bottom left)
- F (back bottom right)
- G (back top right)
- H (back top left)
Step 3: Identify the Face Diagonal
The face diagonal we are interested in is AC. The capacitors connected to these points are:
- AB, AD (connected to A)
- BC, CD (connected to C)
Step 4: Simplify the Circuit
When looking at the face diagonal AC, we can simplify the circuit by considering the symmetry of the cube. The capacitors connected to A and C can be grouped based on their connections.
Step 5: Analyze the Connections
1. From point A, there are two capacitors leading to points B and D.
2. From point C, there are two capacitors leading to points B and D as well.
Step 6: Calculate the Equivalent Capacitance
- The capacitors AB and AD are in parallel, and their equivalent capacitance CAB,AD is:
CAB,AD=C+C=2C
- Similarly, the capacitors BC and CD are also in parallel, giving:
CBC,CD=C+C=2C
Step 7: Combine the Results
Now, we have two branches (from A to B and A to D) leading to C:
- The equivalent capacitance from A to C can be seen as two capacitors CAB,AD and CBC,CD in series:
CAC=11CAB,AD+1CBC,CD=112C+12C=2C2=C
Step 8: Final Calculation
Since we have three paths from A to C, we can combine them:
- The total equivalent capacitance across the face diagonal AC is:
Ceq=C+C+C=3C
Conclusion
The equivalent capacitance across one of the face diagonals of the cube is:
Ceq=4C3
We have a cube where each edge has a capacitor of capacitance C. We need to find the equivalent capacitance across one of the face diagonals, say from point A to point C.
Label the vertices of the cube as follows:
- A (front bottom left)
- B (front bottom right)
- C (front top right)
- D (front top left)
- E (back bottom left)
- F (back bottom right)
- G (back top right)
- H (back top left)
The face diagonal we are interested in is AC. The capacitors connected to these points are:
- AB, AD (connected to A)
- BC, CD (connected to C)
When looking at the face diagonal AC, we can simplify the circuit by considering the symmetry of the cube. The capacitors connected to A and C can be grouped based on their connections.
1. From point A, there are two capacitors leading to points B and D.
2. From point C, there are two capacitors leading to points B and D as well.
- The capacitors AB and AD are in parallel, and their equivalent capacitance CAB,AD is:
CAB,AD=C+C=2C
CBC,CD=C+C=2C
Now, we have two branches (from A to B and A to D) leading to C:
- The equivalent capacitance from A to C can be seen as two capacitors CAB,AD and CBC,CD in series:
CAC=11CAB,AD+1CBC,CD=112C+12C=2C2=C
Since we have three paths from A to C, we can combine them:
- The total equivalent capacitance across the face diagonal AC is:
Ceq=C+C+C=3C
The equivalent capacitance across one of the face diagonals of the cube is:
Ceq=4C3
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Textbook Exercise)
11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Additional Exercises)
23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Conceptual Questions
37 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
Knowledge Check
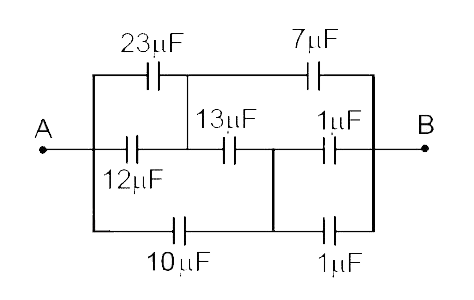
Find the equivalent capacitance across A&B
 A283μFB152μFC15μFDNone
A283μFB152μFC15μFDNoneFind the equivalent capacitance across A and B.
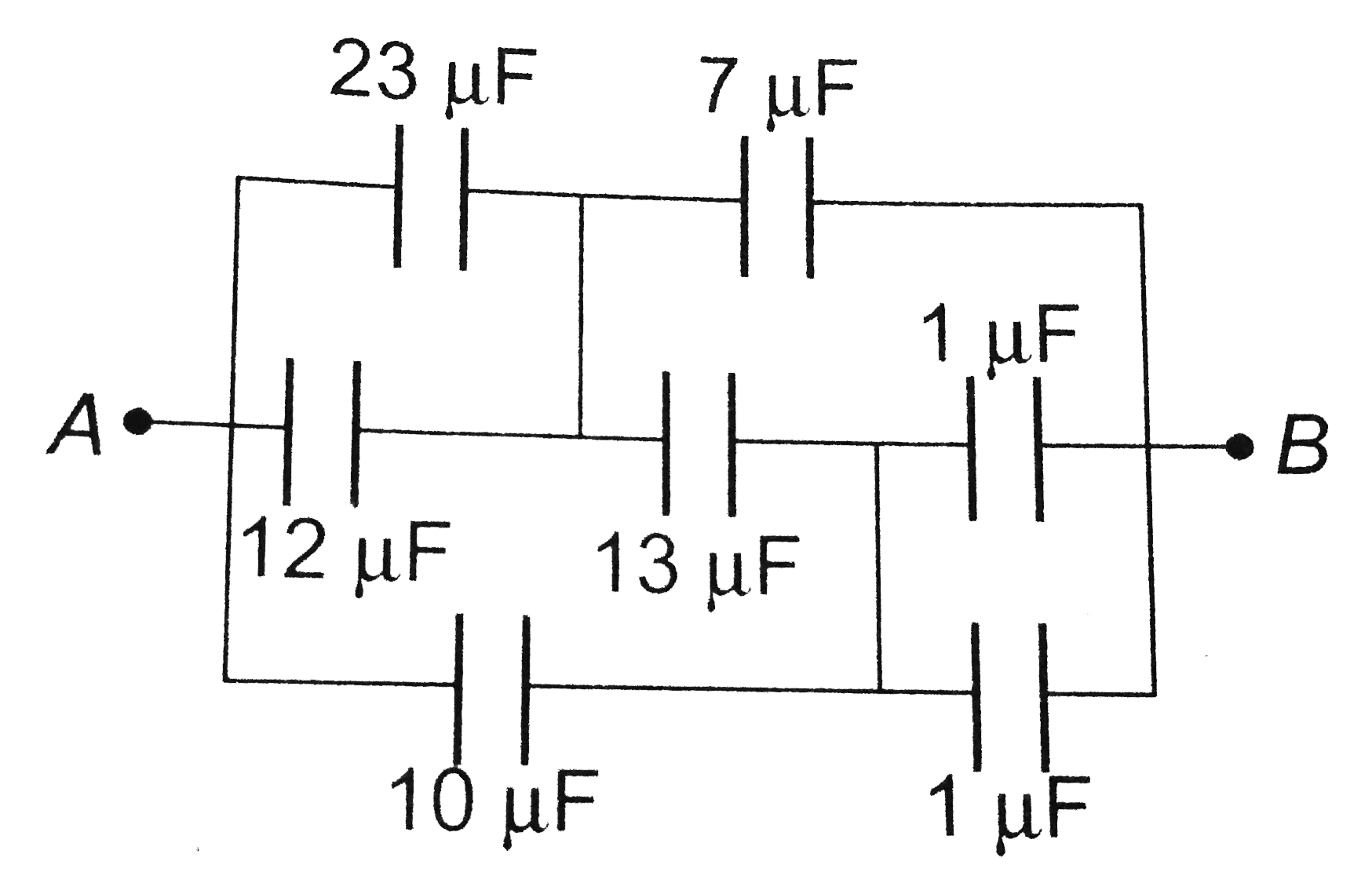
 .A356μFB256μFC15μFDnone of these
.A356μFB256μFC15μFDnone of theseThere are 10 identical capacitors each of capacitance C.
AIf all of them are connected in series, their equivalent capacitance is C/10BIf all of them are connected in parallel, their equivalent capacitance is 10CCIf two series combinations each having 5 capacitors are connected in parallel, their equivalent capacitance is 2C/5DIf they are connected as five parallel combinations each one having two capacitors in series, their equivalent capacitance is 5C/2.
Find the equivalent capacitance across points A and B.
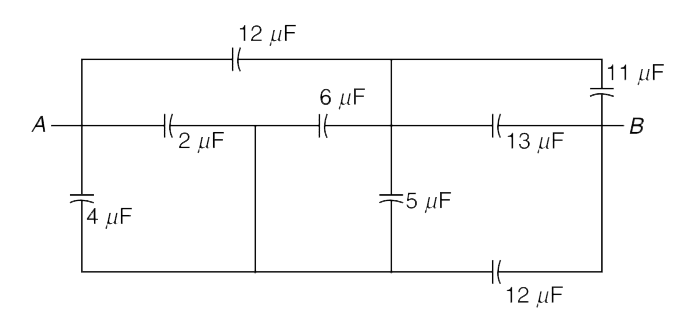
View SolutionTwelve capacitors, each having a capacitance C, are connected to form a cube . Find the equivalent capacitance between the diagonally opposite corners such as A and B.

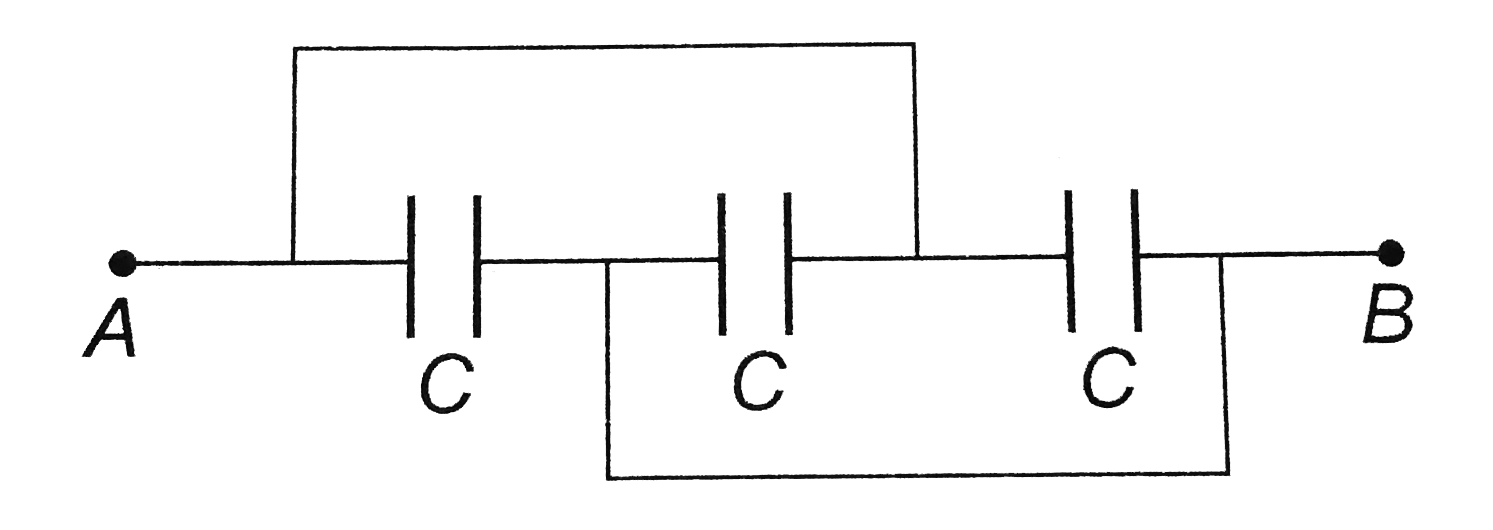
View SolutionThree equal capacitors, each with capacitance C are connected as shown in figure. Then the equivalent capacitance between A and B is
View SolutionFind equivalent capacitance across AB (all capacitances in μF)
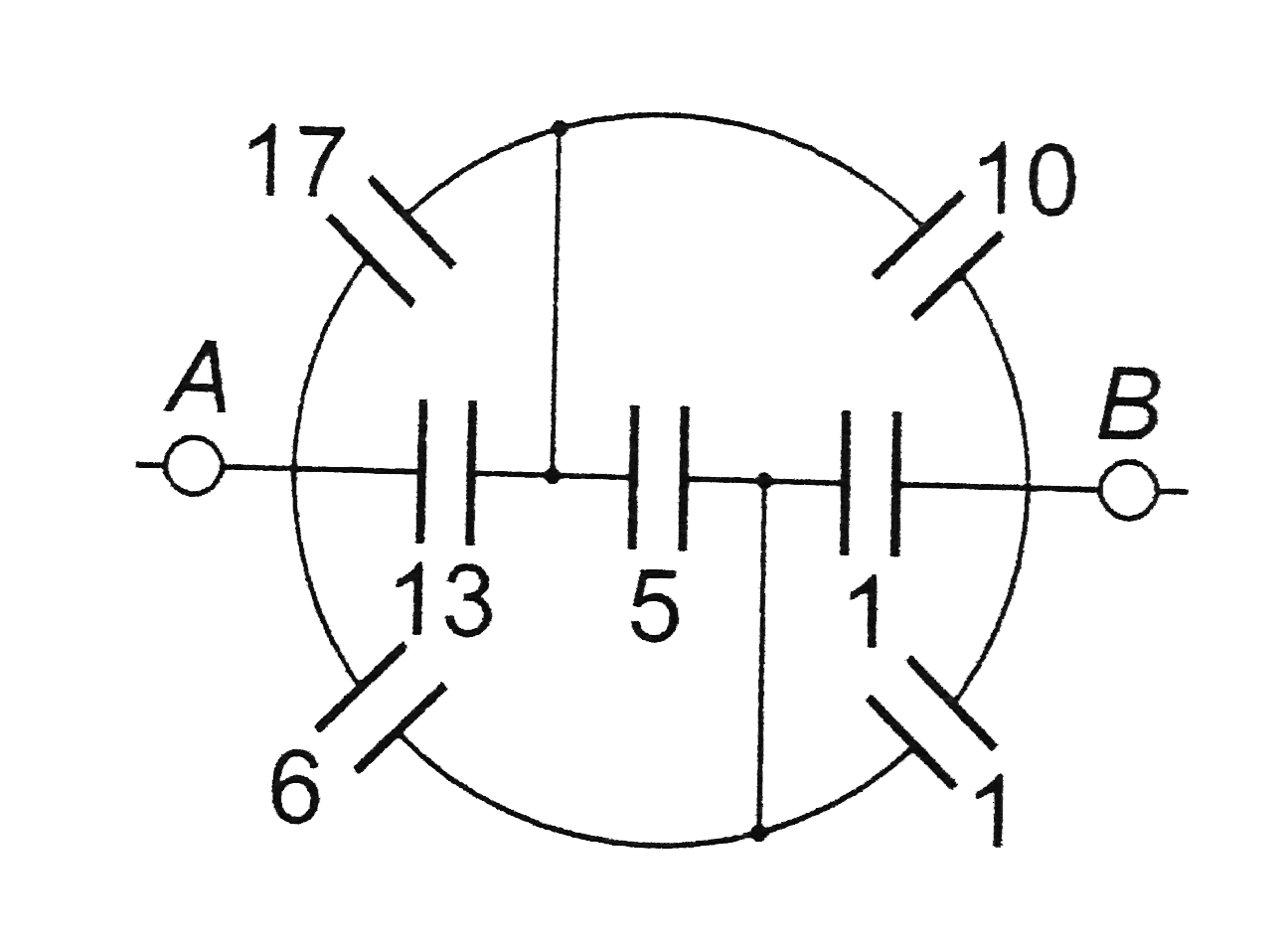
View SolutionAn infinite number of identical capacitors each of capacitance 1mF are connected as shown in the figure. Then the equivalent capacitance between A and B is.
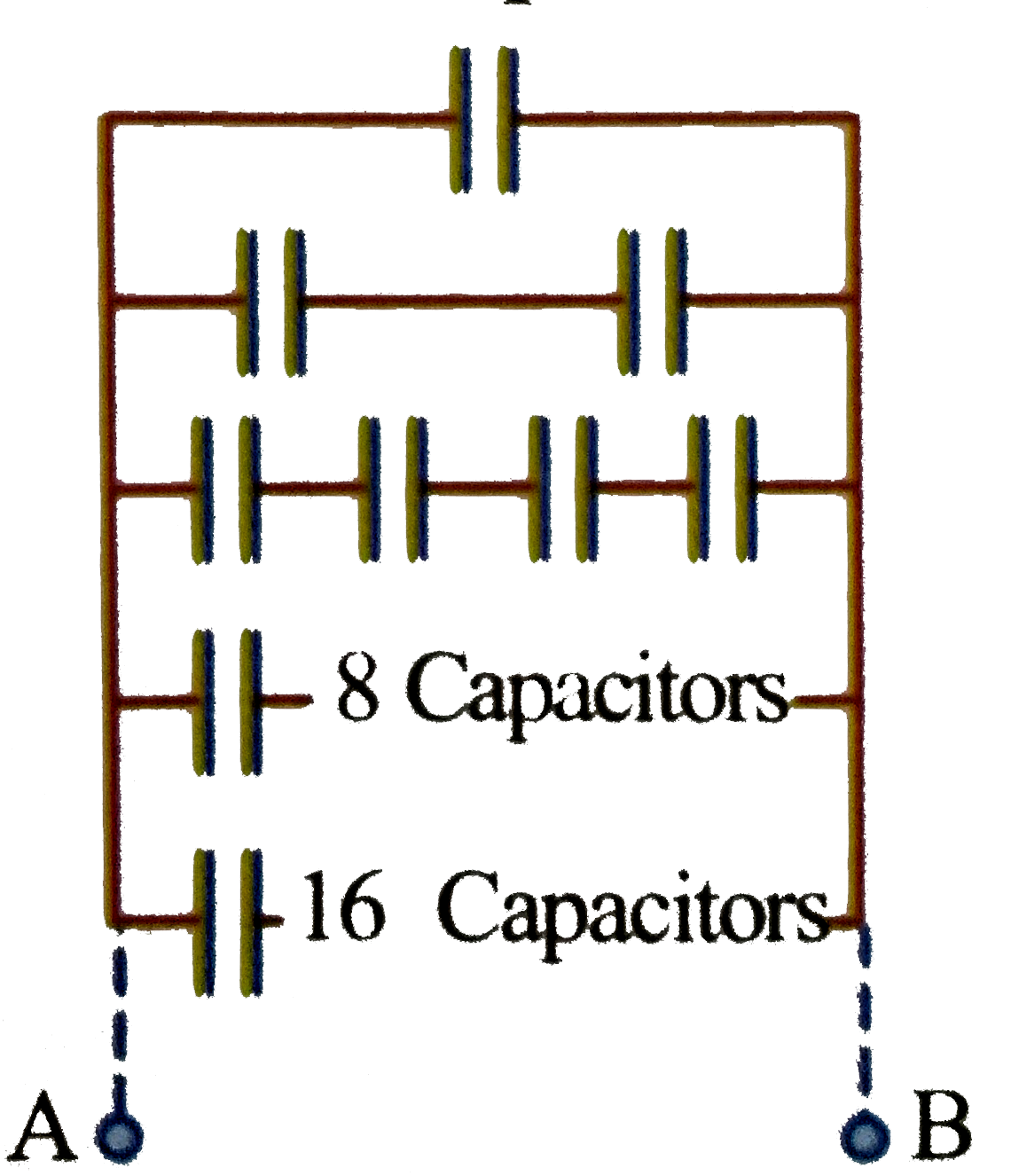 .
.
View Solution