A conducting light string is wound on the rim of a metal ring of radius r and mass m. The free end of the string is fixed to the ceiling. A vertical infinite smooth conducting plane is always tangent to the ring as shown in the figure. A uniform magnetic field Bis applied perpendicular to the plane of the ring. The ring is always inside the magnetic field. The plane and the strip are connected by a resistance R. When the ring is released, find

a. the curent in the resistance R as as function of time.
b. the terminal velocity of the ring.
The correct Answer is:B, D
Let at time t velocity of ring be v (downwards)
e=Bv(2r)=2Bvr
(Two batteries of emf 2Bvr are connect in parallel)
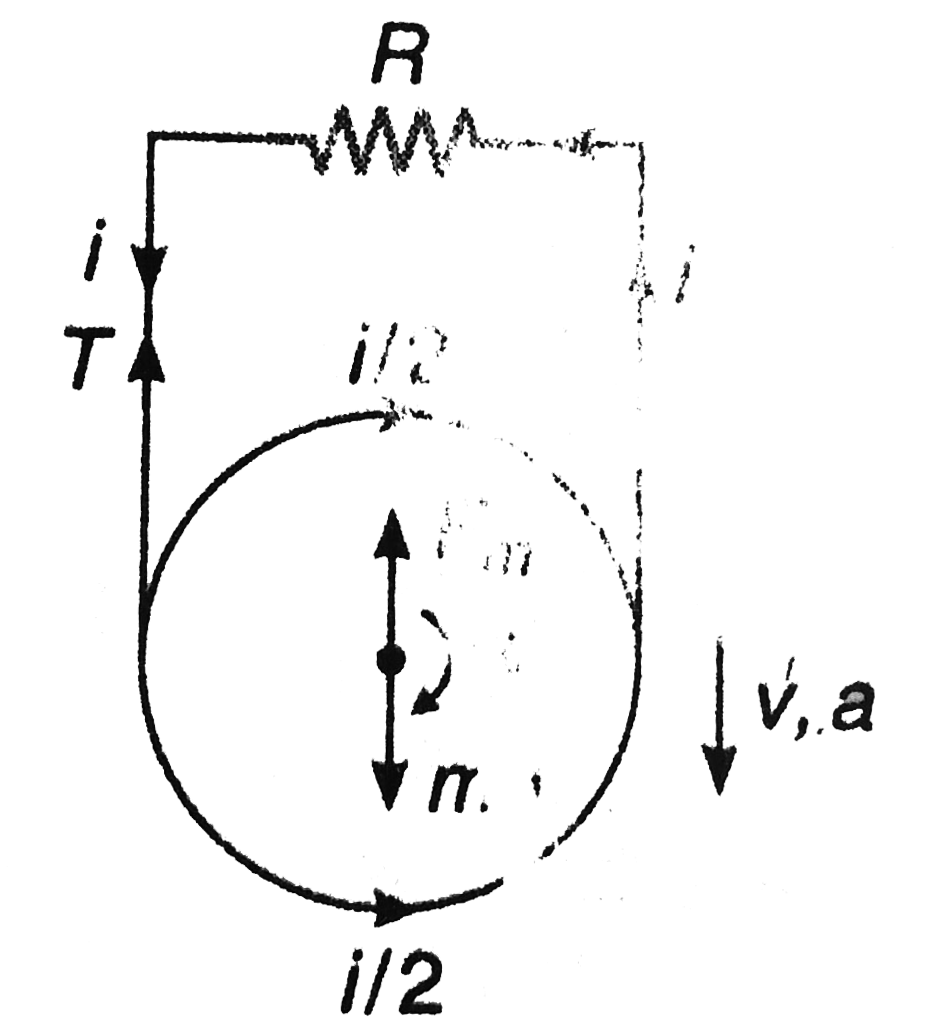
∴i=eR=2BvrR
Now, a=mg−Fm−Tm
Here Fm=2[(i2)(2r)B]=2irB−4B2r2vR
∴a=g−4B2r2vmR−Tm.............(i)
α=Trmr2=Tmr .............(ii)
a=rα=Tm...............(iii)
From Eqn (i) ,( ii) and (iii) we get
a=g2−2B2l2vmR
or ∫v0dvg2−2B2r2vmr=∫10dt
or v=mgR4B2r2(1−e−2B2r2mR)
i=2BvrR=mg2Br(1−e−2B2r2mRt)
and vr=mgR4B2r2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - SUBJECTIVE TYPE
1 Video
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
The magnetic flux linked with a vector area →A in a uniform magnetic field →B is
View SolutionL, C and R represent the physical quantities, inductance, capacitance and resistance respectively. The combination(s) which have the dimensions of frequency are
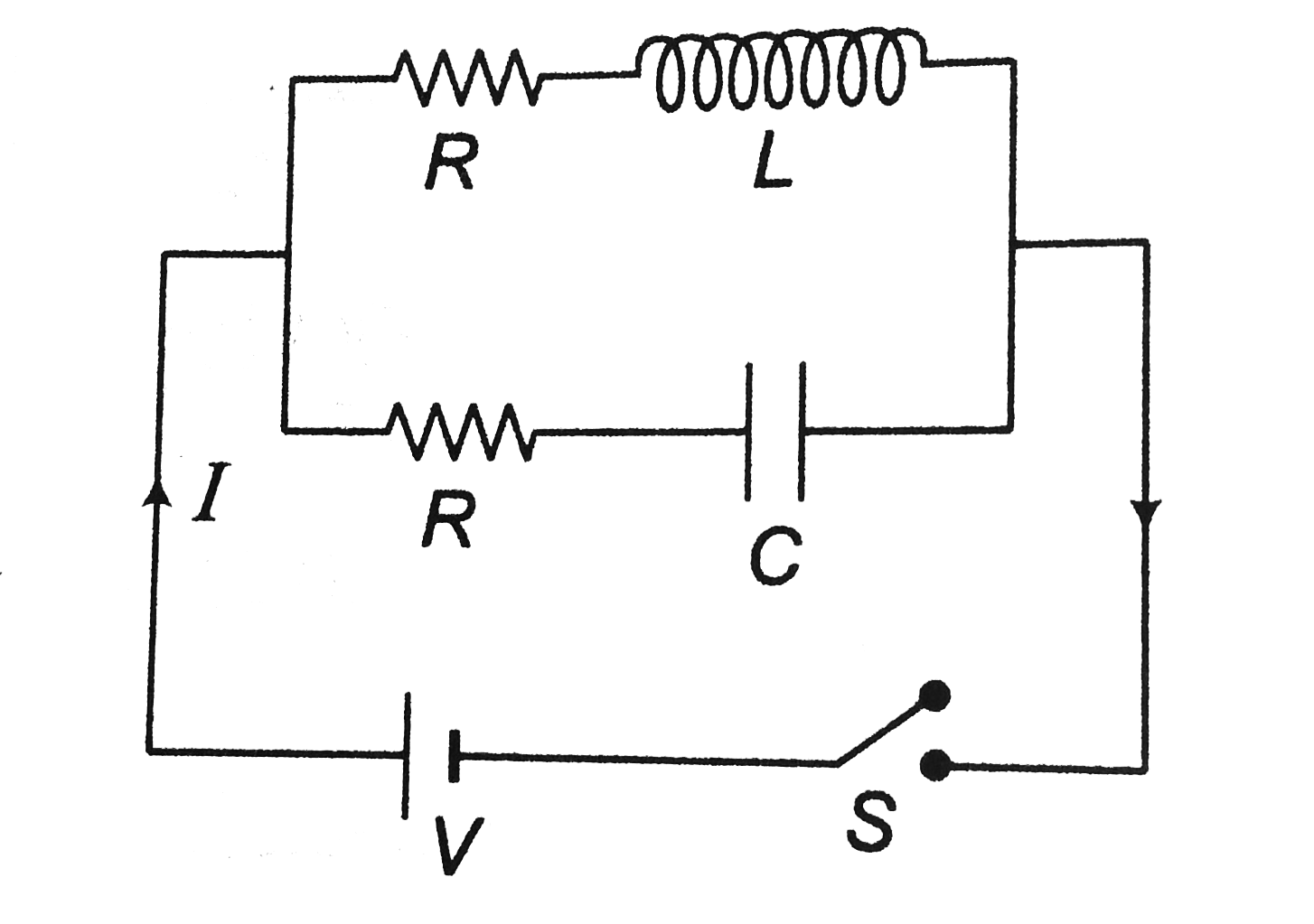
View SolutionIn the circuit diagram shown, initially there is no energy in the inductor and the capacitor, The switch is closed at t=0. Find the current I as a function of time if R=√L/C
View SolutionA potentiometer wire is 100cm long hand a constant potential difference is maintained across it. Two cells are connected in series first to support one another and then in opposite direction. The balance points are obatined at 50cm and 10cm from the positive end of the wire in the two cases. The ratio of emfs is:
View SolutionOut of the following options which one can be used produce a propagating electromagnetic wave?
View SolutionA vertical conducting ring of radius R falls vertically with a speed V in a horizontal uniform magnetic field B which is perpendicular to the plane of the ring. Which of the following statements is correct?
View SolutionA circular conducting ring of radius 'a' is rolling with slipping on a horizontal surface as shown. A uniform magnetic field B is existing perpendicular to the plane of motion of the ring. The emf iniduced between the points A and D of the ring is
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r change ate the rate (dB)/(dt)
View SolutionA conducting ring of radius 2R rolls on a smooth horizontal conducting surface as shown in figure-5.295. A uniform horizontal magnetic field B is perpendicular to the plane of the ring. The potential of A with respect to O is:
View SolutionA conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
View SolutionA ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field. Find the instant of time at which EMF will be maximum & minimum respectively. (Figure: )
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate. (dB)/(dt) . Then
View SolutionA conducting ring of radius r is placed in a varying magnetic field perpendicular to the plane of the ring. If the rate at which the magnetic field varies is x, the electric field intensity at any point of the ring is
View SolutionA ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field. Find the instant of time at which EMF will be maximum & minimum respectively. (Figure: )
View Solution