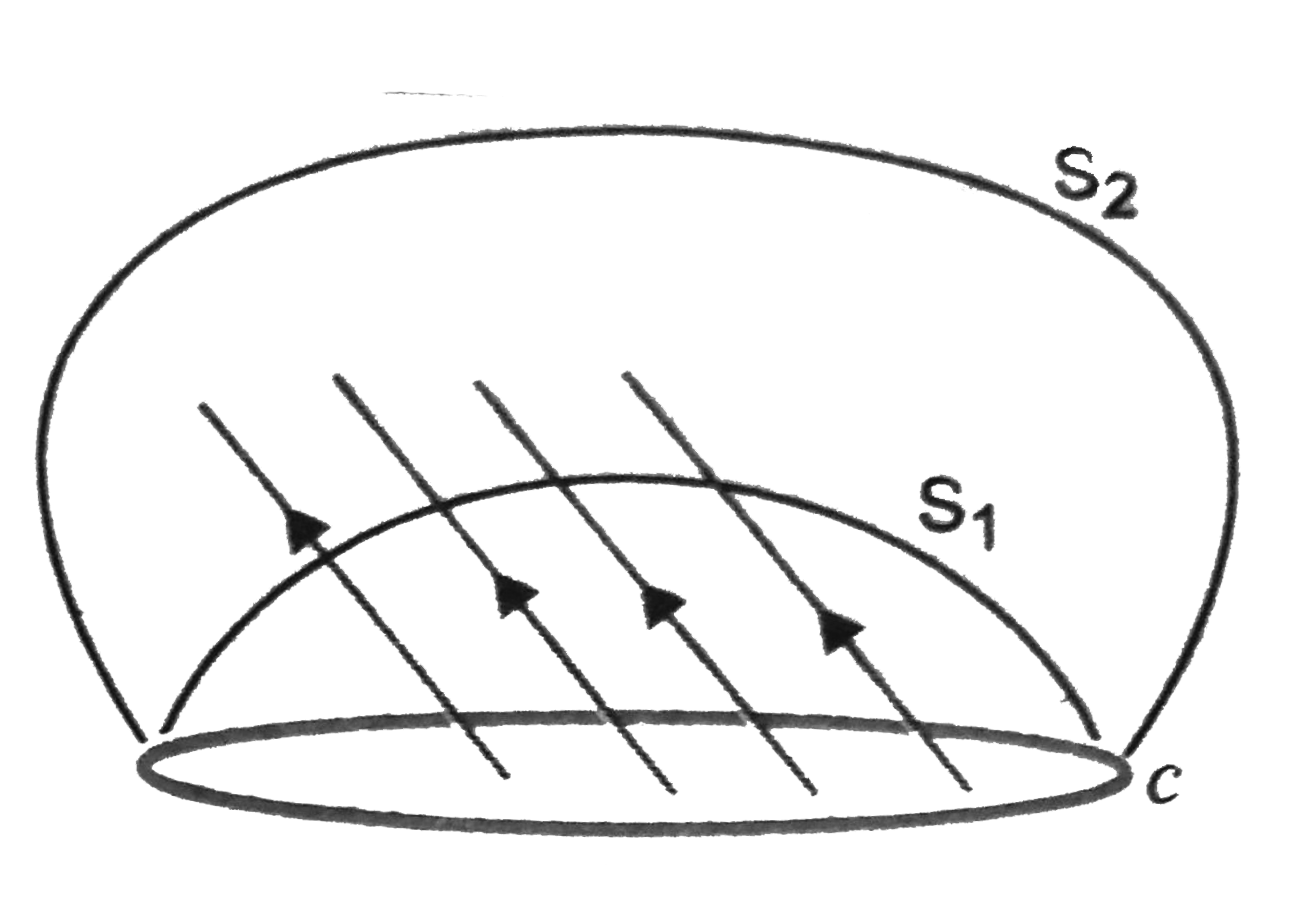
Consider a closed loop C in a magnetic field (refer to the given figure). The flux passing through the loop is defined by choosing a surface whose edge coincide's with the loop and using the formula ϕ=−→B1.d−→A1+−→B2.d−→A2+... Now if we choose two different surfaces S1 and S2 having C as their edge, would we get the same answer for flux. Justify your answer.

The amount of flux associated with both the surfaces is same. Flux is defined as the number of magnetic field lines passing through the surface. The magnetic field lines cannot end or start in space as they form closed loops. Hence, the number of lines passing through surface S1 must be the same as the number of lines passing through the surface S2.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - HIGHER ORDER THINKING SKILLS AND ADVANCED LEVEL8videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - REVISION EXERCISE (Very Short Answer Questions Carrying I mark)44videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTIONS) (Very short answer type questions)6videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test15videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
Similar Questions
Consider a closed loop C in a magnetic field, Fig. The flux passing through the loop is defined by choosing a surface whose edge coincides with the loop and using the formula ϕ=B1.dA1+B2.Da2+……..Now if we chose two different surfaces S1 and S2 having C as their edge, would we get the same answer for flux. Justify your answer.
 View Solution
View SolutionConsider a closed loop C in a magnetic field, Fig. The flux passing through the loop is defined by choosing a surface whose edge coincides with the loop and using the formula ϕ=B1.dA1+B2.Da2+……..Now if we chose two different surfaces S1 and S2 having C as their edge, would we get the same answer for flux. Justify your answer.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
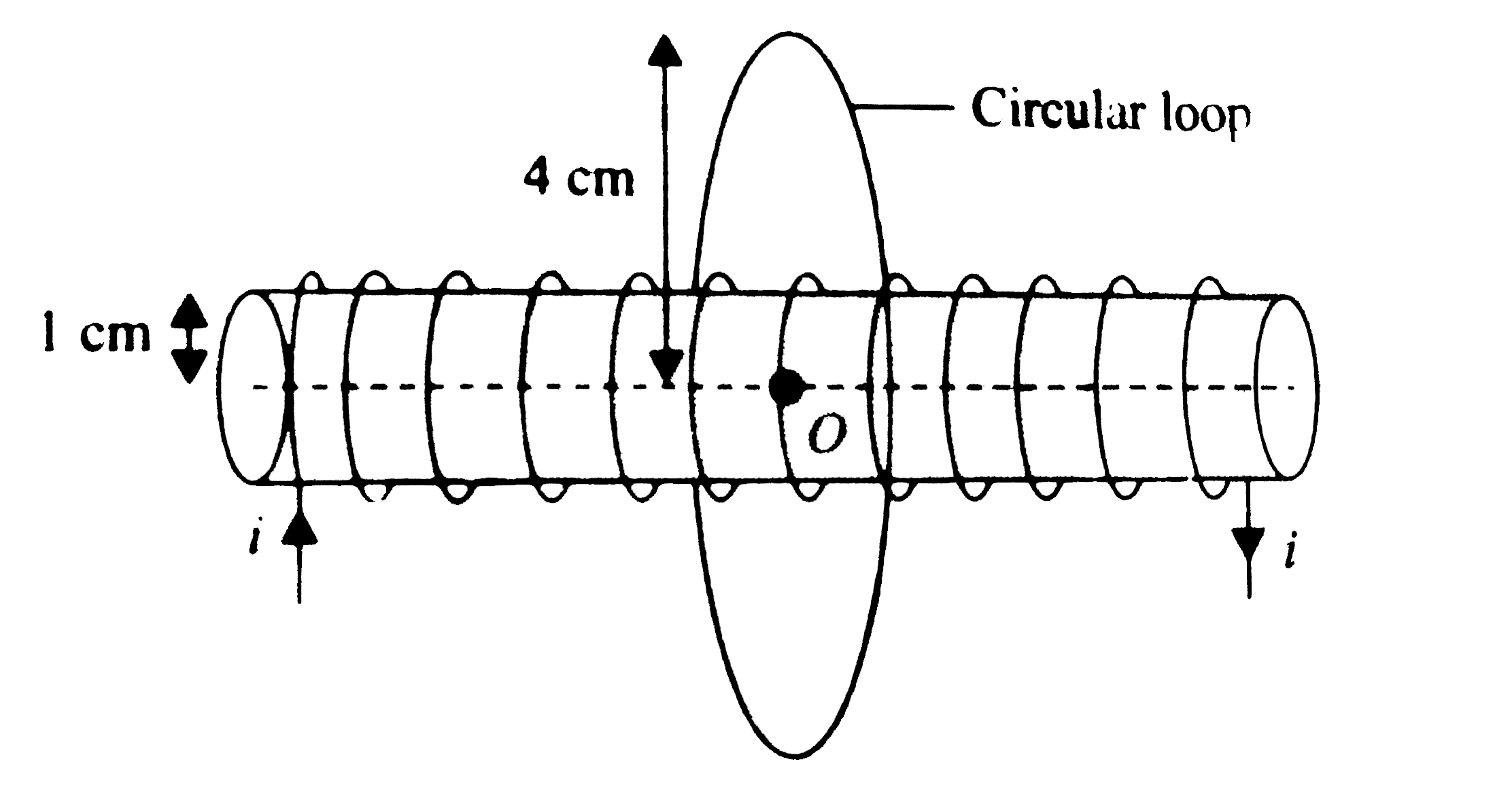
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoidAμ0ni(πa21)Bμ0ni(πa22)CzeroDμ0ni(πa21+πa22) - Question 2 - Select One
A closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as →μ=−→IA where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field →B, then torque acting on the loop is given by →τ=→μ×→B. Now answer the following questions:
Consider the situation shown in Fig., ring is having a uniformly distributed positive charge. Magnetic field is perpendicular to the axis of ring. Now ring is rotated in anticlockwise direction as seen from left hand side direction of magnetic torque acting on the ring is
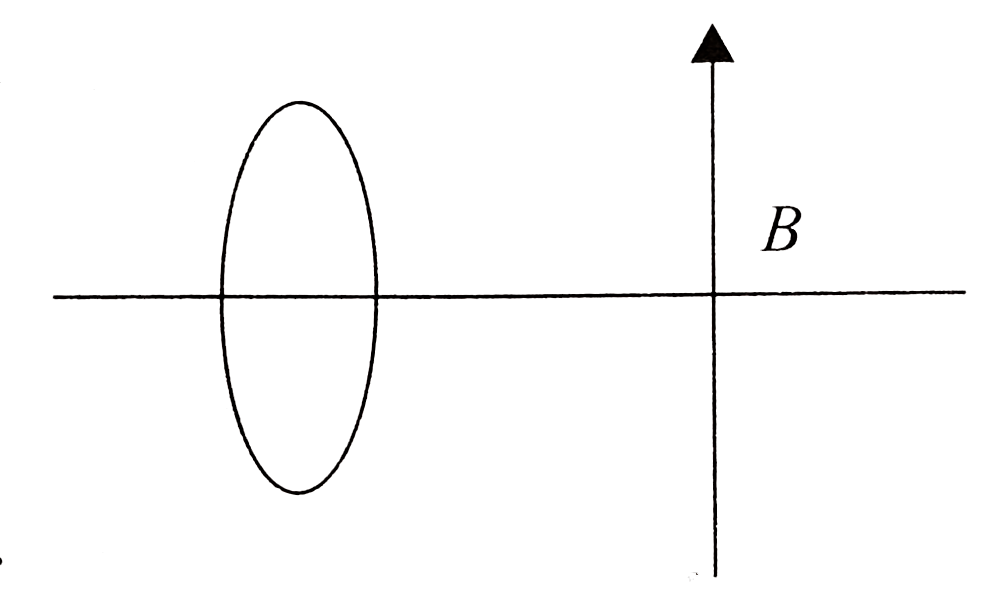 AParallel to →BBParallel to axis of ringCGoing into plane of paperDComing out of plane of paper
AParallel to →BBParallel to axis of ringCGoing into plane of paperDComing out of plane of paper
The magnetic field in a certain region is given by B=(4.0→i−1.8→k)×10−3T. How much flux passes through a 5.0cm2 area loop in this region if the loop lies flat on the xy-plane?
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoidView SolutionA closed current carrying circular loop is placed on one face of a cubical box as shown in fig. The magnetic flux through area of the box contained by the loop is ϕ1 and the magnetic flux through remaining surface area of the box is ϕ2 . What is relation between them
 View Solution
View SolutionA closed current carrying circular loop is placed on one face of a cubical box as shown in fig. The magnetic flux through area of the box contained by the loop is ϕ1 and the magnetic flux through remaining surface area of the box is ϕ2 . Which of the following option is correct
 View Solution
View SolutionA closed current carrying circular loop is placed on one face of a cubical box as shown in fig. The magnetic flux through area of the box contained by the loop is ϕ1 and the magnetic flux through remaining surface area of the box is ϕ2 . Which of the following option is correct
 View Solution
View SolutionA closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as →μ=−→IA where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field →B, then torque acting on the loop is given by →τ=→μ×→B. Now answer the following questions:
Consider the situation shown in Fig., ring is having a uniformly distributed positive charge. Magnetic field is perpendicular to the axis of ring. Now ring is rotated in anticlockwise direction as seen from left hand side direction of magnetic torque acting on the ring is
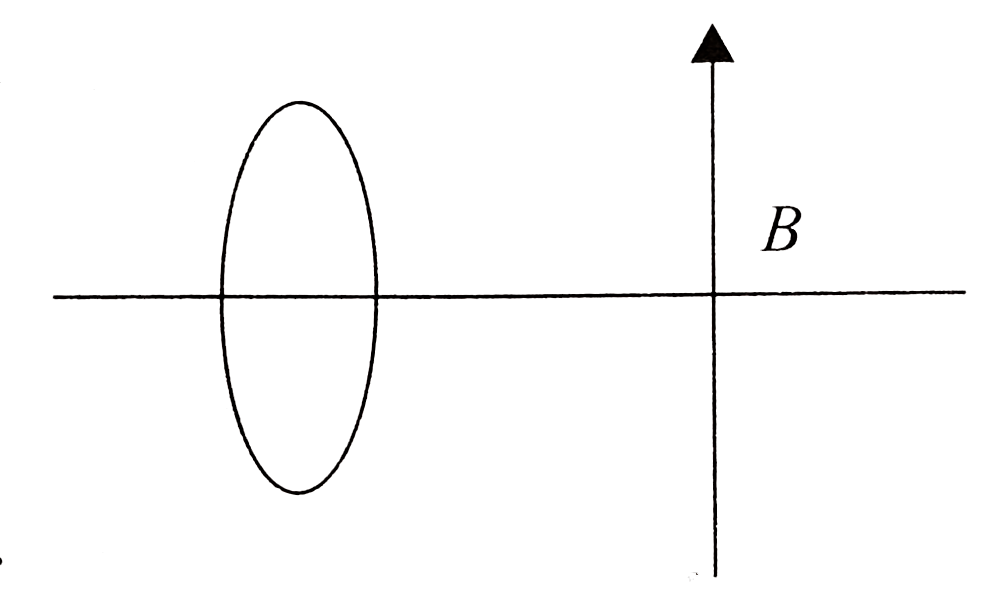 View Solution
View Solution

