A capacitor of capacitance 200μF is connected to a battery through a resistance of 5kΩ at time t = 0. Charge stored in the capacitor in first second in larger than the charge stored in the next
1s
10s
100 s
1,000 s
The correct Answer is:A, B, C, D
To solve the problem, we need to analyze the charging behavior of a capacitor connected to a resistor and a battery. The key points to consider are the capacitance, resistance, and the time constant of the circuit.
1. Identify Given Values:
- Capacitance (C) = 200 µF = 200 × 10^(-6) F
- Resistance (R) = 5 kΩ = 5000 Ω
2. Calculate the Time Constant (τ):
The time constant τ for an RC circuit is given by the formula:
τ=R×C
Substituting the values:
τ=5000Ω×200×10−6F=1s
3. Understand the Charging Equation:
The charge (Q) on a capacitor at time t during charging is given by:
Q(t)=C⋅V⋅(1−e−t/τ)
where V is the voltage of the battery and e is the base of the natural logarithm.
4. Calculate Charge at t = 1 second:
At t = 1 s, the charge stored in the capacitor is:
Q(1)=C⋅V⋅(1−e−1/1)=C⋅V⋅(1−e−1)
5. Calculate Charge at t = 2 seconds:
At t = 2 s, the charge stored is:
Q(2)=C⋅V⋅(1−e−2/1)=C⋅V⋅(1−e−2)
6. Compare Charges:
We need to compare Q(1) and Q(2):
- Since e−1 is approximately 0.3679 and e−2 is approximately 0.1353, we have:
Q(1)=C⋅V⋅(1−0.3679)=C⋅V⋅0.6321
Q(2)=C⋅V⋅(1−0.1353)=C⋅V⋅0.8647
- Clearly, Q(1)<Q(2) since 0.6321 < 0.8647.
7. Conclusion:
The charge stored in the capacitor in the first second is less than the charge stored in the next second. Therefore, the statement in the question is incorrect.
- Capacitance (C) = 200 µF = 200 × 10^(-6) F
- Resistance (R) = 5 kΩ = 5000 Ω
The time constant τ for an RC circuit is given by the formula:
τ=R×C
Substituting the values:
τ=5000Ω×200×10−6F=1s
The charge (Q) on a capacitor at time t during charging is given by:
Q(t)=C⋅V⋅(1−e−t/τ)
where V is the voltage of the battery and e is the base of the natural logarithm.
At t = 1 s, the charge stored in the capacitor is:
Q(1)=C⋅V⋅(1−e−1/1)=C⋅V⋅(1−e−1)
At t = 2 s, the charge stored is:
Q(2)=C⋅V⋅(1−e−2/1)=C⋅V⋅(1−e−2)
We need to compare Q(1) and Q(2):
- Since e−1 is approximately 0.3679 and e−2 is approximately 0.1353, we have:
Q(1)=C⋅V⋅(1−0.3679)=C⋅V⋅0.6321
Q(2)=C⋅V⋅(1−0.1353)=C⋅V⋅0.8647
- Clearly, Q(1)<Q(2) since 0.6321 < 0.8647.
The charge stored in the capacitor in the first second is less than the charge stored in the next second. Therefore, the statement in the question is incorrect.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS BASED ON A GIVEN PASSAGE/COMPREHENSION)
Explore 15 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (D. MULTIPLE CHOICE QUESTIONS ASSERTION REASON TYPE QUESTIONS)
Explore 10 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION JEE (ADVANCED) FOR IIT ENTRANCE)
Explore 9 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
Knowledge Check
A 20 μF capacitor is connected to 45 V battery through a circuit whose resistance is 2000 Ω. What is the final charge on the capacitor ?
A9×10−4CB9 154×10−4CC98×10−4CDNone of these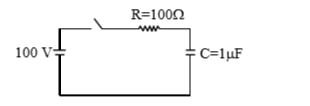
A capacitor of capacitance C=1 μF is suddenly connected to a battery of 100 volt through a resistance R=100Ω . The time taken for the capacitor to be charged to get 50 V is :
[Take ln 2 = 0.69]A1.44×10−4sB3.33×10−4sC0.69×10−4sD0.30×10−4sA capacitor of capacitance 10μF is charged by connecting through a resistance of 20Omga and battery of 20 V. What is the energy supplied by the battery?
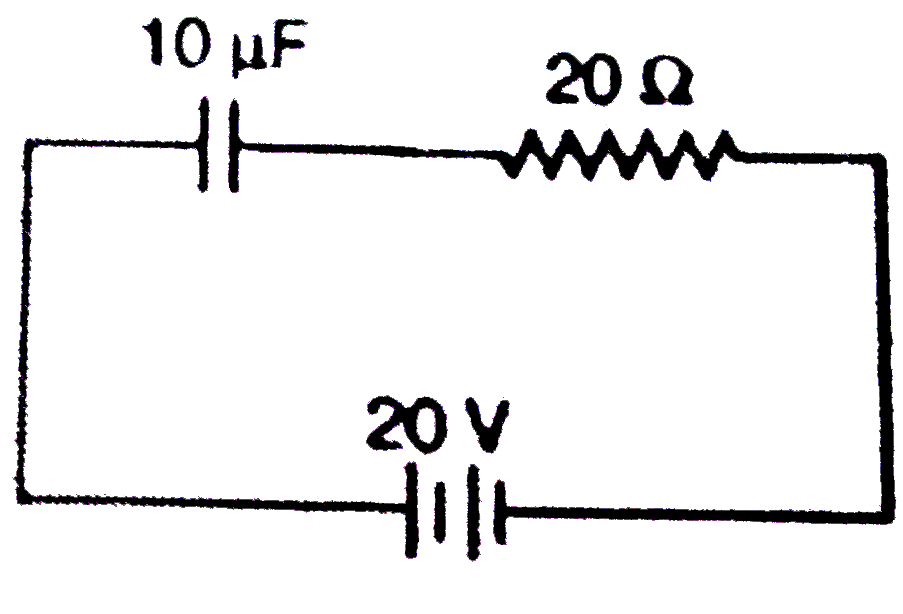 ALess than 2 mJBEqual to 2 mJCMore than 2 mJDCannot be predicted
ALess than 2 mJBEqual to 2 mJCMore than 2 mJDCannot be predicted
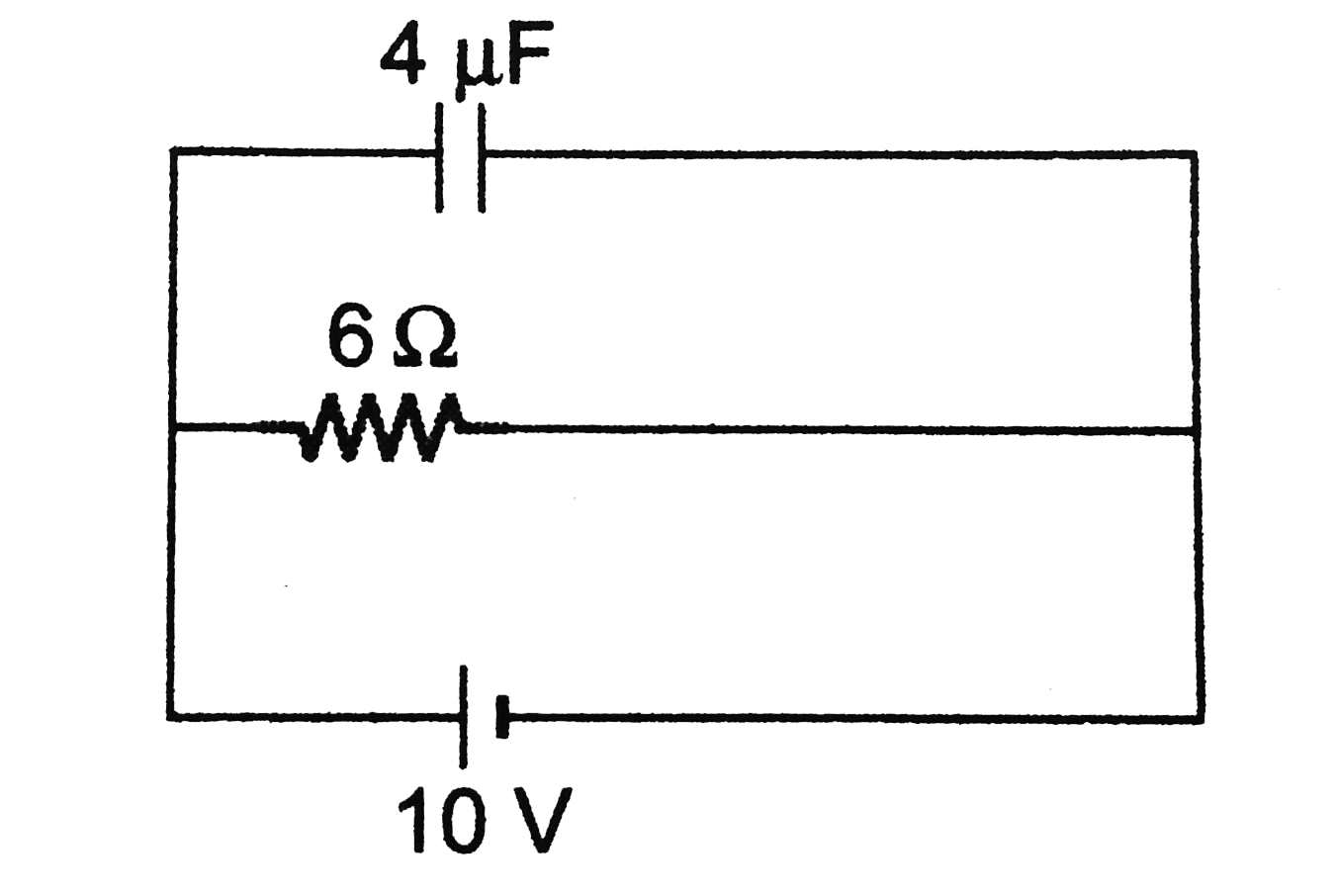
Find the charge stored in the capacitor.
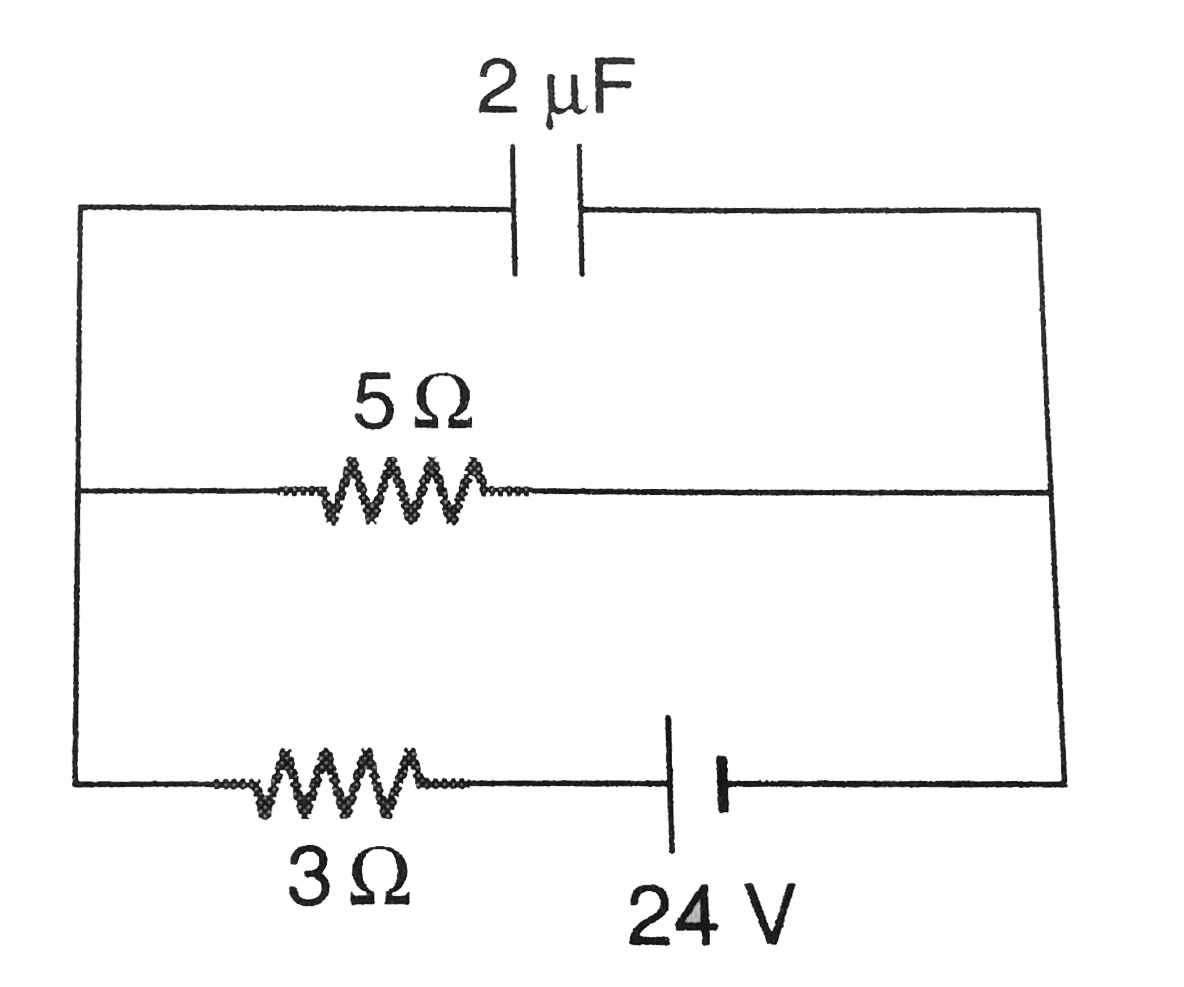
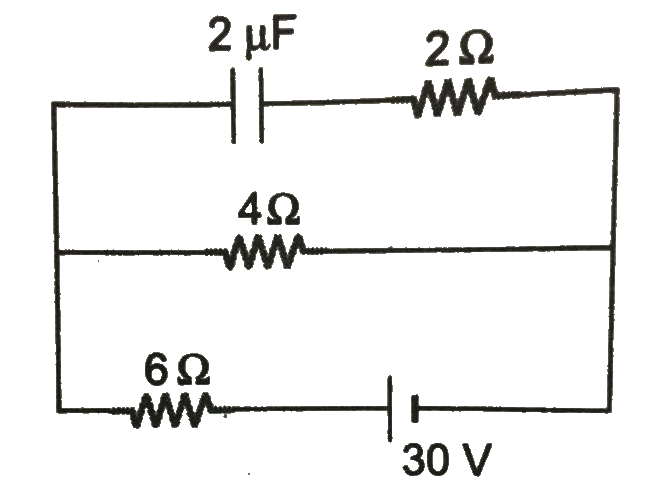
View SolutionA capacitor of capacitance 500(μ)Fis connected to a battery through a (10k(Ω)) resistor.The charge stored on the capacitance 2(μ)F are separately charged by a common battery for a long time. The two capacitors are then separately discharged through equal resistors.Both the discharge circuits are connected at t=0.
View SolutionA capacitor of capacitance C is connected to a battery of emf (ε)at t=0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate has this maximum value?
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :
View SolutionA capcitor of capacitance 1300μF is connected to a battery of 300V and charged. Then the energy stored in the condenser is
View Solution