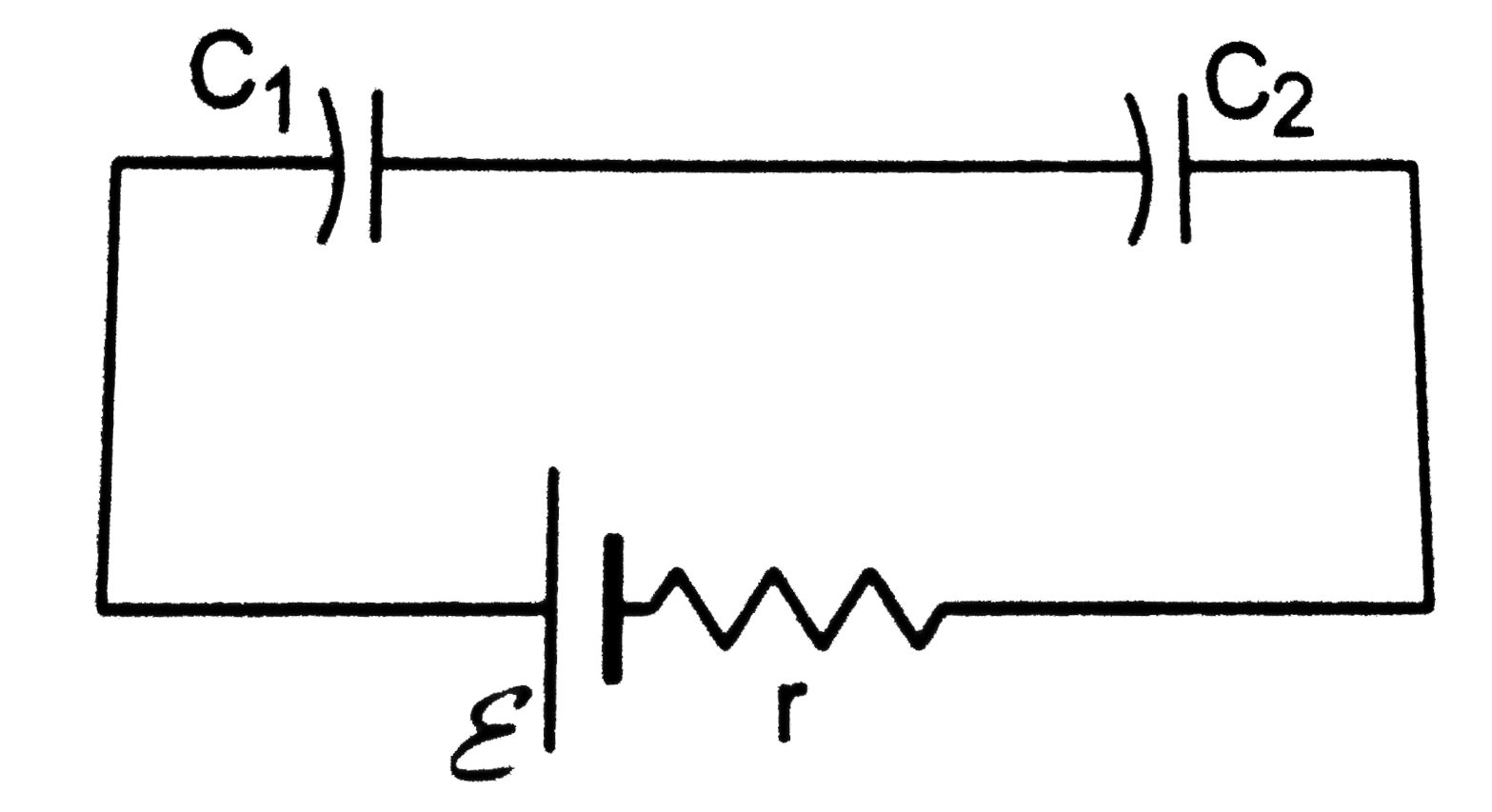
In the following circuit th switch S is closed at t = 0 . The charge on the capacitor C1 as a fouction of time will be given by (Ceq=C1C2C1+C2)

C2 E[1−exp(−eR/C1)]
CeqEexp(−t/RCeq)
CeqE[1−exp(−t/RCeq)]
C2E[1−exp(−t/RC2)]
The correct Answer is:C
(c ) Circuit equivalent to given RC circuit is

Same charge is stored by both the capacitors as these are connected in series . Charge as a function of time is given by
Q=CepE[1−e−t/RCeq
Hence option ( c) is correct.
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE JEE (ADVANCED ) FOR IIT ENTRANCE
4 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE C. MULTIPLE CHOICE QUESTIONS
17 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS) B. MULTIPLE CHOICE QUESTIONS
15 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
Similar Questions
In the following circuit, the switch S is closed at t = 0. The charge on the capacitor C1 as a function of time will be given by (Ceq=C1C2C1+C2)

View SolutionIn the following circuit, the switch S is closed at t = 0. The charge on the capacitor C1 as a function of time will be given by (Ceq=C1C2C1+C2)

View Solution
Knowledge Check
In the given circuit switch is closed at t=0. The charge flown in time t=Tc (where Tc is time constant).
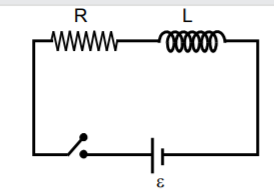 AεLR2eBεLR2C(εL)(1−1e)RDεLR
AεLR2eBεLR2C(εL)(1−1e)RDεLRIn the given circuit C1=C,C2=2C,C3=3C. If charge at the capacitor C2 is Q. Then the charge at the capacitor C3 will be
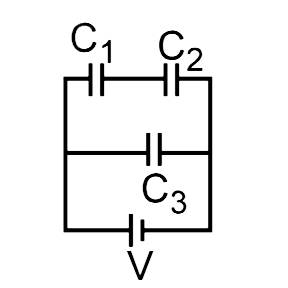 A3Q2B9Q2CQ3DQ6
A3Q2B9Q2CQ3DQ6The capacitor C1 in the figure shown initially carries a charge q0. When the switches S1 and S2 are closed, capacitor C1 is connected in series to a resistor R and a second capacitor C2 which is initially uncharged.

The charge flown through wires as a function of time is
where C=C1C2C1+C2Aq0e−tRC+CC2q0Bq0CC1x[1−e−tRC]Cq0CC1e−tCRDq0e−tRC
Consider the situation shown in figure.The switch is closed at t=0when the capacitor C1as a function of time t.
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant

View SolutionIn the given circuit switch is closed at t=0. The charge flown in time t=Tc (where Tc is time constant).

View SolutionWhen switch is closed , charges on C1andC2 are
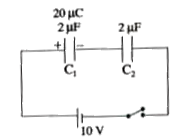
View SolutionIn the circuit shown below the switch is closed at t=0. For 0<t<R(C1+C2), the current I1 in the capacitor C1 in terms of total current I is

View Solution
