The refractive index of plastic is √3. Calculate the angle of refraction for a ray of light incident at polarizing angle.
To solve the problem of finding the angle of refraction for a ray of light incident at the polarizing angle when the refractive index of plastic is √3, we can follow these steps:
Step 1: Understand Brewster's Law
Brewster's Law states that at the polarizing angle Ip, the refractive index μ of the medium is given by:
μ=tanIp
where Ip is the polarizing angle.
Step 2: Calculate the Polarizing Angle
Given that the refractive index of plastic is √3, we can set up the equation:
√3=tanIp
To find Ip, we take the inverse tangent:
Ip=tan−1(√3)
From trigonometric values, we know:
tan(60∘)=√3
Thus,
Ip=60∘
Step 3: Apply Snell's Law
Snell's Law relates the angles of incidence and refraction to the refractive indices of the two media:
μ1sinI=μ2sinr
Here, μ1=1 (for air), I=Ip=60∘, and μ2=√3 (for plastic). We need to find r.
Substituting the known values into Snell's Law:
1⋅sin(60∘)=√3⋅sin(r)
Step 4: Calculate sin(60∘)
We know:
sin(60∘)=√32
Substituting this into the equation gives:
√32=√3⋅sin(r)
Step 5: Solve for sin(r)
Dividing both sides by √3:
12=sin(r)
Step 6: Find the Angle of Refraction
Now, we find r using the inverse sine function:
r=sin−1(12)
From trigonometric values, we know:
sin(30∘)=12
Thus,
r=30∘
Conclusion
The angle of refraction for a ray of light incident at the polarizing angle is:
30∘
---
Brewster's Law states that at the polarizing angle Ip, the refractive index μ of the medium is given by:
μ=tanIp
where Ip is the polarizing angle.
Given that the refractive index of plastic is √3, we can set up the equation:
√3=tanIp
To find Ip, we take the inverse tangent:
Ip=tan−1(√3)
From trigonometric values, we know:
tan(60∘)=√3
Thus,
Ip=60∘
Snell's Law relates the angles of incidence and refraction to the refractive indices of the two media:
μ1sinI=μ2sinr
Here, μ1=1 (for air), I=Ip=60∘, and μ2=√3 (for plastic). We need to find r.
1⋅sin(60∘)=√3⋅sin(r)
We know:
sin(60∘)=√32
Substituting this into the equation gives:
√32=√3⋅sin(r)
Dividing both sides by √3:
12=sin(r)
Now, we find r using the inverse sine function:
r=sin−1(12)
From trigonometric values, we know:
sin(30∘)=12
Thus,
r=30∘
The angle of refraction for a ray of light incident at the polarizing angle is:
30∘
Topper's Solved these Questions
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - Revision Exercises (Additional Questions)
12 Videos
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - Revision Exercises (Fill in the Blanks)
10 Videos
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - Higher Order Thinking Skills & Advanced Level (QUESTIONS WITH ANSWERS)
8 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
The refractive index of a medium is √3. What is the angle of refraction, if unpolarizing light is incident on the polarising angle of the medium ?
View SolutionThe refractive index of a medium is √3. What is the angle of refraction, if the unpolarised light is incident on it at the polarising angle of the medium ?
View Solution
Knowledge Check
The ray of light travels from raer medium to denser medium of refractive index μ. The angle of incidence of twice the angle of refraction. The angle of incidence is given by
A2sin−1(μ2)B2cos−1(2μ)C2cos−1(μ2)Dsin−1(μ2)A ray of light passes from vacuum into a medium of refractive index n . If the angle of incidence is twice the angle of refraction , then the relation between the angle of incidence and the refractive index is
An=2sin(i2)Bn=2cos(i2)Cn=2tan(i2)Dn=12[cos(i2)]A ray of light passes from vaccume into a medium of refractive index n. if the angle of incidence is twice the angle of refraction, then the angle of incidence is
Acos−10.8Bsin−10.8C2cos−10.8D2sin−10.8
The refractive index of a medium is √3. What is the angle of refraction, if polarizing angle of the medium.
View SolutionWhen sun light is incident at an angle of 53∘ on the surface of water, the reflected light is plane polarized. Calculate the angle of refraction and refractive index of water.
View SolutionCalculate the angle of emergence (e) of the ray of light incident normally on the face AC of a glass prism ABC of refractive index √3. How will the angle of emergence change qualitatively, if the ray of light emerges from the prism into a liquid of refractive index 1.3 instead of air ?
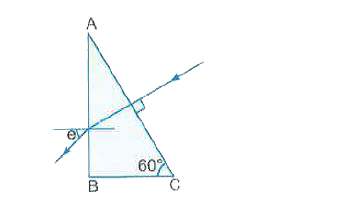
View SolutionRefractive index of a prism is √7/3 and the angle of prism is 60∘. The minimum angle of incidence of a ray that will be transmitted through the prism is
View SolutionA ray of light passes from vacuum of 3×108m/s medium of refractive index μ, the angle of incidence is found to be twice the angle of refraction. Then the angle of incidence is:
View Solution
