The average life of a radioactive sample is 100 millisecond. A charged capacitor having capacitance 200 μF is connected across a resistance R. For what value of R, the ratio of charge on capacitor to the activity of the sample remains constant with time or independent of time.
To solve the problem, we need to find the value of the resistance R such that the ratio of the charge on the capacitor to the activity of the radioactive sample remains constant over time.
1. Understand the Average Life and Decay Constant:
The average life τ of a radioactive sample is related to the decay constant λ by the formula:
τ=1λ
Given that τ=100 milliseconds, we can convert this to seconds:
τ=100×10−3 s=0.1 s
Therefore, the decay constant λ is:
λ=1τ=10.1=10 s−1
2. Charge on the Capacitor:
The charge Q on a capacitor discharging through a resistor R is given by:
Q(t)=Q0e−tRC
where Q0 is the initial charge and C is the capacitance.
3. Activity of the Radioactive Sample:
The activity A of the radioactive sample at time t is given by:
A(t)=A0e−λt
where A0 is the initial activity.
4. Ratio of Charge to Activity:
We need to find the ratio Q(t)A(t):
Q(t)A(t)=Q0e−tRCA0e−λt=Q0A0e(−tRC+λt)
For this ratio to be independent of time, the exponent must equal zero:
−tRC+λt=0
This simplifies to:
1RC=λ
5. Finding Resistance R:
Rearranging the equation gives:
R=1λC
Substituting λ=10s−1 and C=200μF=200×10−6F:
R=110×200×10−6=12×10−4=5000Ω
Final Answer:
The required resistance R is 5000Ω or 5kΩ.
The average life τ of a radioactive sample is related to the decay constant λ by the formula:
τ=1λ
Given that τ=100 milliseconds, we can convert this to seconds:
τ=100×10−3 s=0.1 s
Therefore, the decay constant λ is:
λ=1τ=10.1=10 s−1
The charge Q on a capacitor discharging through a resistor R is given by:
Q(t)=Q0e−tRC
where Q0 is the initial charge and C is the capacitance.
The activity A of the radioactive sample at time t is given by:
A(t)=A0e−λt
where A0 is the initial activity.
We need to find the ratio Q(t)A(t):
Q(t)A(t)=Q0e−tRCA0e−λt=Q0A0e(−tRC+λt)
For this ratio to be independent of time, the exponent must equal zero:
−tRC+λt=0
This simplifies to:
1RC=λ
Rearranging the equation gives:
R=1λC
Substituting λ=10s−1 and C=200μF=200×10−6F:
R=110×200×10−6=12×10−4=5000Ω
The required resistance R is 5000Ω or 5kΩ.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - REVISION EXERCISES (VERY SHORT ANSWER QUESTIONS)47videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - REVISION EXERCISES (ADDITIONAL QUESTIONS CARRYING 1 MARK)8videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - NCERT FILE SOLVED (NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTIONS (SHORT ANSWER TYPE QUESTIONS))5videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - CHAPTER PRACTICE TEST13videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - CHAPTER PRACTICE TEST14videos
RAY OPTICS AND OPTICAL INSTRUMENTS
Similar Questions
A radioactive sample decays with an average life of 20ms. A capacitor of capacitance 100μF is charged to some potential and then the plates are connected through a resistance R. What should be the value of R so that the ratio of the charge on the capacitor to the activity of the radioactive sample remains constant in time?
View SolutionA radioactive sample has an average life of 30 ms and is decaying. A capacitor of capacitance 200 μF is first charged and later connected with resistor 'R'. If the ratio of charge on capacitor to the activity of radioactive sample is fixed with respect to time then the value of 'R' should be ______Ω.
View Solution
Knowledge Check
- Question 1 - Select One
Average life ofa radioactive sample is 4 ms Initially the total number of nuclie is N0 A charged capacitor of capacity 20μf is connected across a resistor R. The value of R such that ratio of number of nuclei remaining to the charge on capacitor remains constant with time is
A100ΩB200ΩC300ΩD400Ω - Question 2 - Select One
A charged capacitor of capacitance C is discharging through a resistor of resistance R. At what time the charge on the capacitor is equal to one half of its initial value?
ARC2BRCloge2CRC loge2D1RCloge2 - Question 3 - Select One
Two capacitors A and B having capacitances 10μf and 20μF are connected in series with a 12 V battery. The ratio of the charge on A and B is
A0.5:1B1:1C2:1D2:4
A charged capacitor of capacitance 40μF is discharged through a 50Ω resistance. Determine the time constant of the circuit.
View SolutionA capacitor of 10μF is connected with a resistance of 2.2MΩ. What is the time constant of the circuit.
View SolutionA capacitor of capacitance 100μF discharges through a resistor R. At the same time a radioactive substances decays with mean life 30 ms. If ratio of charge on capacitor and activity of substance does not change with time then find R.
 View Solution
View SolutionA capacitor of capacitance 200μF is connected to a battery through a resistance of 5kΩ at time t = 0. Charge stored in the capacitor in first second in larger than the charge stored in the next
View SolutionA capacitor of capacitance 10μF is charged by connecting through a resistance of 20Omga and battery of 20 V. What is the energy supplied by the battery?
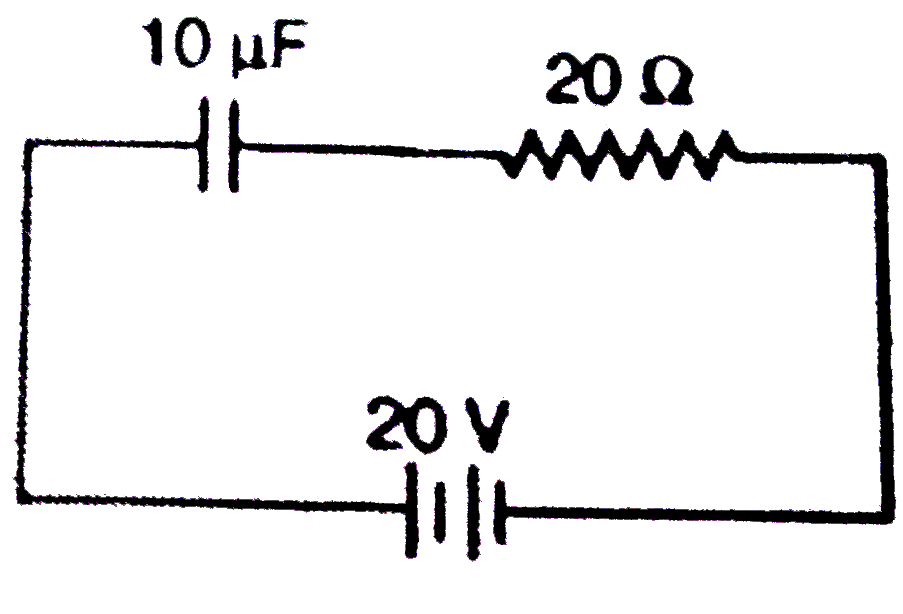 View Solution
View Solution

