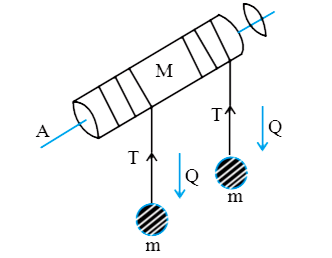
A uniform solid cylinder having mass M and radius R rotates about a horizontal frictionless axle AB. With the help of massless inextensible two ropes are suspended two masses with equal mass m by wrapping the ropes on the cylinder as shown. What will be the tension in each of the rope when masses are released from height 'h' above the ground?

$\frac{M m g}{M + 4 m}$

$\frac{M m g}{M + 3 m}$

$\frac{M m g}{M + 2 m}$

None of these

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

A uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?

A $\frac{M m g}{M + m}$
B $\frac{M m g}{M + 2 m}$
C $\frac{M m g}{M + 3 m}$
D $\frac{M m g}{M + 4 m}$
A solid cylinder of mass M and of radius R is fixed on a frictionless axle over a well. A rope negligible mass is wrapped around the cylinder. A bucket of uniform mass m is suspended from it. The linear acceleration bucket will:
A $\frac{4 m g}{M + 2 m}$
B $\frac{4 m g}{M + 4 m}$
C $\frac{2 m g}{M + m}$
D $\frac{2 m g}{M + 2 m}$
A solid cylinder of mass M and of radius R is fixed on a frictionless axle over a well. A rope negligible mass is wrapped around the cylinder. A bucket of uniform mass m is suspended from it. The linear acceleration bucket will:
A $\frac{m g}{M + m}$
B $\frac{2 m g}{M + m}$
C $\frac{2 m g}{M + 2 m}$
D $\frac{2 m g}{2 M + m}$