Two metal rods of same length have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross-sections A1 and A2 respectively. What is the condition for the same rates of flow of heat ? Solution in Kannada
K1K2=A1A2
K1K2=A2A1
K21A22=K22A21
K1A21=K2A22
The correct Answer is:D
Q1t=k1A1(T1−T2)d
Q2t=k2A2(T1−T2)d
Now Q1t=Q2t
⇒k1A1(T1=T2)d=k1A2(T1−T2)d
⇒ k1k2=A2A1
Thus correct choice is (b)
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - TRANSFERENCE OF HEAT EXERCISE - Multiple Choice Questions (Level - III) Questions From AIEEE/JEE Examination)5videos
TRANSFERENCE OF HEAT
- BOOK - MODERN PUBLICATIONCHAPTER - TRANSFERENCE OF HEAT EXERCISE - Recent Competitive Questions4videos
TRANSFERENCE OF HEAT
- BOOK - MODERN PUBLICATIONCHAPTER - TRANSFERENCE OF HEAT EXERCISE - Recent Competitive Questions4videos
TRANSFERENCE OF HEAT
- BOOK - MODERN PUBLICATIONCHAPTER - SOLIDS & SEMICONDUCTOR DEVICESEXERCISE - Revision Test28videos
SOLIDS & SEMICONDUCTOR DEVICES
- BOOK - MODERN PUBLICATIONCHAPTER - UNIFORM CIRCULAR MOTIONEXERCISE - Revision Test57videos
UNIFORM CIRCULAR MOTION
Similar Questions
A composite block is made of slabs A,B,C,D and E of different thermal conductivities (given in terms of a constant K) and sizes (given in terms of length, L) as shown in the figure. All slabs are of same width. Heat 'Q' flows only from left to right through the blocks.
Then in steady state
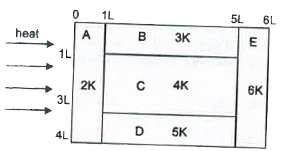 02:46View Solution
02:46View SolutionTwo slabs are of the thicknesses d1 and d2. Their thermal conductivities are K1 and K2 respectively They are in series. The free ends of the combination of these two slabs are kept at temperatures θ1 and θ2. Assume θ1>θ2. The temperature θ of their common junction is
01:57View SolutionTwo slabs are of the thicknesses d1 and d2. Their thermal conductivities are K1 and K2 respectively They are in series. The free ends of the combination of these two slabs are kept at temperatures θ1 and θ2. Assume θ1>θ2. The temperature θ of their common junction is
02:40View SolutionChoose the forward biased p-n junction :
01:06View SolutionA sphere of mass m is tied to end of a string of length 1 and rotated through the other and along a horizontal circular path with speed . The work done in full horizontal circle is:
View SolutionTwo rods one is semi circular of thermal conductivity K_(1) and otheir is straight of thermal conductivity K_(2) and of same cross sectional area are joined as shown in the The points A and B are maintained at same temperature difference. If rate of flow of heat is same in two rods then K_(1)//K_(2) is .
02:42View SolutionTwo rods A and B are of equal lengths. Their ends of kept between the same temperature and their area of cross-section are A1 and A2 and thermal conductivities K1 and K2. The rate of heat transmission in the two rods will be equal, if
03:17View SolutionTwo rods of same length and area of cross-section A_(1)" and" A_(2) have their ends at the same temperature. If K_(1) "and" K_(2) are their thermal conductivities, c_(1) "and" c_(2) are their specific heats and d_(1) "and "d_(2) are their densities, then the rate of flow of heat is the same in both the rods if
04:04View SolutionEqual temperature difference exists between the ends of two metallic rods 1 and 2of equal length. Their thermal conduetivities are K1 and K2 and cross sectional areas are respectively A1 and A2. The condition for equal rate of heat transfer will be-
02:23View SolutionCondider two rods of same length and different specific heats (s_(1), s_(2)) , thermal conductivities (K_(1), K_(2)) and areas of cross-section (A_(1), A_(2)) and both having temperatures (T_(1), T_(2)) at their ends. If their rate of loss of heat due to conduction are equal, then
03:33View SolutionTwo rods P and Q of equal lengths have thermal conductivities K_(1) and K_(2) and cross-sectional areas A_(1) and A_(2) respectively. If the temperature difference across the ends of each rod is the same, then the condition for which the rate of flow of heat through each of them will be equal, is
02:19View SolutionTwo different metal rods of the same length have their ends kept at the same temperature theta_(1) , and theta_(2) with theta_(2) gt theta_(1) . If A_(1) and A_(2) are their cross-sectional areas and K_(1) and K_(2) their thermal conductivities, the rate of flow of heat in the two rods will be the same it:
View SolutionTwo metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View SolutionEqual temperature difference exists between the ends of two metallic rods 1 and 2 of equal lengths. Their thermal conductivity is K_(1) and K_(2) and cross-sectional areas are respectively A_(1) and A_(2) . The condition for equal rate of heat transfer will be
01:50View SolutionTwo rods A and B are of equal lengths. Their ends are kept at the same temperature difference and their area of cross - sections are A_(1) and A_(2) and thermal conductivities k_(1) and k_(2) . The rate of heat transmission in two rods will be equal, if . . . .. . .
01:48View Solution

