f(x)={x−1,−1≤x≤0x2,0≤x≤1andg(x)=sinx
Consider the functions h1(x)=f(|g(x)|)andh2(x)=|f(g(x))|.
Which of the following is not true about h2(x)?
A
The domain is R
B
It is periodic with period 2π.
C
The range is [0, 1].
D
None of these
Video Solution
Text Solution
The correct Answer is:C
|g(x)|=|sinx|,x∈R
f(|g(x)|)={|sinx|−1,−1≤|sinx|<0(|sinx|)2,0≤(|sinx|)≤1=sin2x,x∈R
f(g(x))={sinx−1,−1≤sinx<0sin2x,0≤sinx≤1
={sinx−1,(2n−1)π<x<2nπsin2x,2nπ≤x≤(2n+1)π,n∈Z.
or |f(g(x))|={sinx−1,(2n−1)π<x<2nπsin2x,2nπ≤x≤(2n+1)π,n∈Z.
h2(x)=|f(g(x))| has domain R.
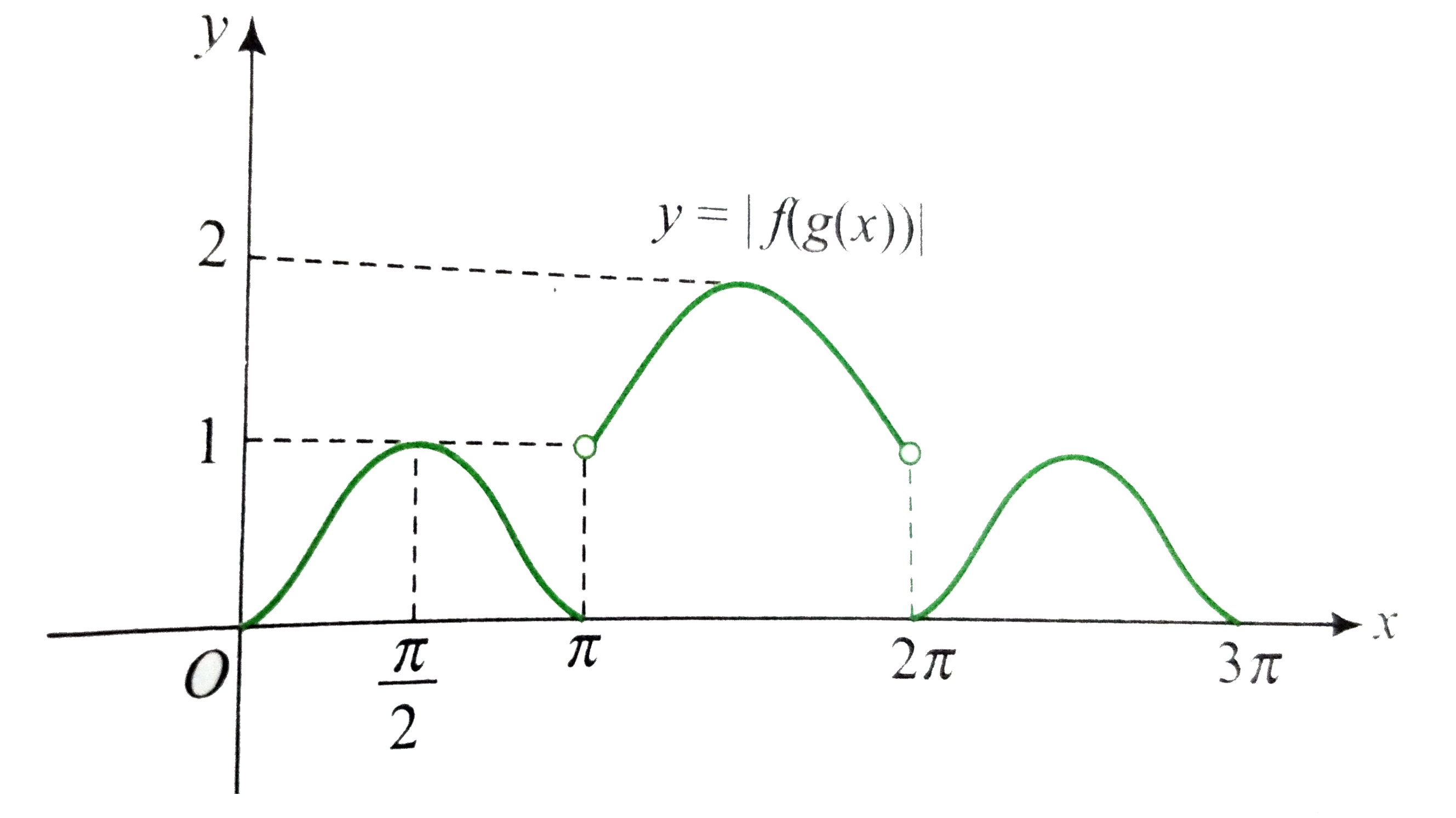
Also , from the graph, it is periodic with period 2π and has range [0, 2].
|
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)
9 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Numerical)
31 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Multiple)
27 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
31 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Knowledge Check
f(x)={x−1,−1≤x≤0x2,0≤x≤1andg(x)=sinx
Consider the functions h1(x)=f(|g(x)|)andh2(x)=|f(g(x))|.
Which of the following is not true about h1(x)?AIt is a periodic function with period π.BThe range is [0, 1].CThe domain is R.DNone of theseConsider the function f(x)=f(x)={x−1,−1≤x≤0x2,0≤x≤1
and g(x)=sinx.
If h1(x)=f(|g(x)|)
and h2(x)=|f(g(x))|.
Which of the following is not true about h1(x)?AIt is a periodic function with period πBThe range is [0, 1]CDomain RDNone of thesef(x)={x−1,−1≤x≤0x2,0≤x≤1andg(x)=sinx
Consider the functions h1(x)=f(|g(x)|)andh2(x)=|f(g(x))|.
If for h1(x)andh2(x) are identical functions, then which of the following is not true?ADomain of h1(x)andh2(x) is x∈[2nπ,(2n+1)π],n∈Z.BRange of h1(x)andh2(x) is [0,1]CPeriod of h1(x)andh2(x) is πDNone of these
Let f(x)={1+x,0≤x≤23−x,2<x≤3
find (fof) (x).
View SolutionLet f(x)={−1,−2≤x<0x2−1,0≤x≤2 and g(x)=|f(x)|+f(|x|). Then in the interval (−2,2), g is
View SolutionIf f(x)={x2+10≤x<1−3x+51≤x≤2
View SolutionLet f(x)={−1−2≤x<0x2−10≤x≤2 and g(x)=|f(x)|+f(|x|). Then , in the interval (-2,2),g is
View SolutionConsider f(x)=|1−x|,1≤x≤2andg(x)=f(x)+bsin.π2x,1≤x≤2 then which of the following is correct?
View Solution
