Doubtnut Promotions Sticky

Let f(x)=f1(x)−2f2(x), where ,where f1(x)={(min{x2,|x|}|x|≤1max{x2,|x|}|x|≤1) and f2(x)={(min{x2,|x|}|x|<1{x2,|x|}|x|≤1) and let g(x)={(min{f(t):−3≤t≤x,−3≤x≤0}max{f(t):0≤t≤x,0≤x≤3}) for −3≤x≤−1 the range of g(x) is

A

[−1,3]

B

[−1,−15]

C

[−1,9]

D

None of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

f1(x)=x2andf2(x)=|x|
orf(x)=f1(x)−2f2(x)=x2−2|x|
Graph of f(x)
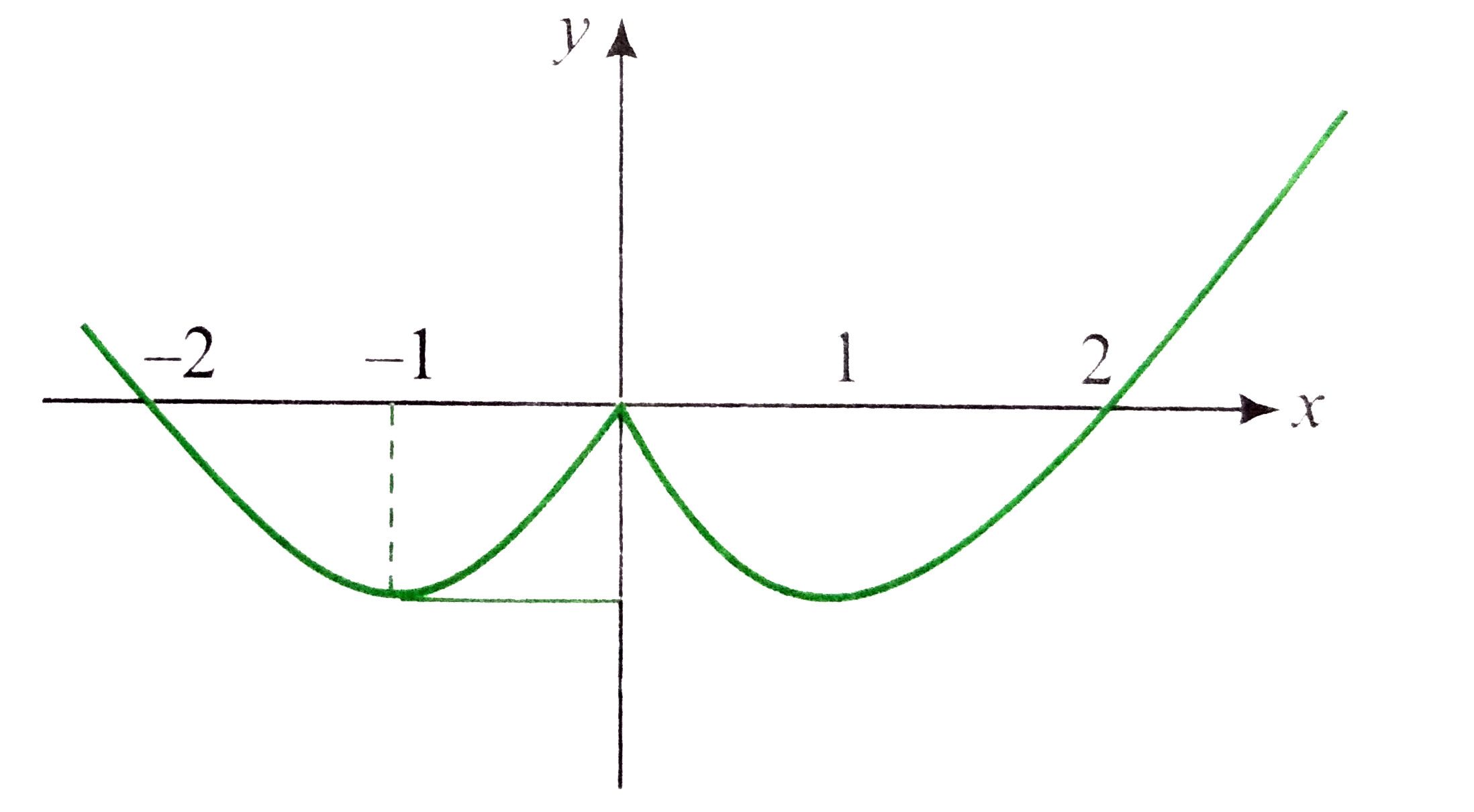
ocr_image
g(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩f(x),−3≤x<−1−1,−1≤x<00,0≤x≤2f(x),2<x≤3=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩x2+2x,−3≤x<−1−1,−1≤x<00,0≤x≤2x2−2x,2<x≤3
The range of g(x) for [-3, -1] is [-1, 3].

|
Updated on:21/07/2023
Class 12MATHSRELATIONS AND FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Let f(x)=f1(x)−2f2(x), where
    where f(x)={min{x2,|x|},|x|≤1max{x2,|x|},|x|>1
    and f2(x)={min{x2,|x|},|x|>1max{x2,|x|},|x|≤1
    and let g(x)={min{f(t):−3≤t≤x, −3≤x<0}max{f(t):0≤t≤x, 0≤x≤3}
    For x∈(−1,0),f(x)+g(x) is

    Ax2−2x+1
    Bx2+2x−1
    Cx2+2x+1
    Dx2−2x−1
  • Question 2 - Select One

    Let f(x)=f1(x)−2f2(x), where
    f1(x)={min{x2,|x|},|x|≤1max{x2,|x|},|x|>1
    and f2(x)={min{x2,|x|},|x|>1max{x2,|x|},|x|≤1
    and let g(x)={min{f(t),−3≤t≤x,−3≤x<0}max{f(t),0≤t<x,0≤x≤3}
    For x∈(−1,00),f(x)+g(x)is

    Ax2−2x+1
    Bx2+2x−1
    Cx2+2x+1
    Dx2−2x−1
  • Question 3 - Select One

    Let f(x)=f1(x)−2f2(x), where f1(x)={min{x2,|x|},|x|≤1max{x2,|x|},|x|>1 and f2(x)={min{x2,|x|},|x|>1max{x2,|x|},|x|≤1 and let g(x)={min{f(t),−3≤t≤x,−3≤x<0}max{f(t),0≤t<x,0≤x≤3} The graph of y=g(x) in its domain is broken at

    A1 point
    B2 points
    C3 points
    DNone of these