Consider a function f whose domain is [-3, 4] and range is [-2, 2] with following graph.
Consider a function f whose domain is [-3, 4] and range is [-2, 2] with following graph. If h(x)=|f(x)-(3)/(2)| has range [e, f] and n be number of real solutions of h(x)=(1)/(4),
If h(x)=∣∣∣f(x)−32∣∣∣ has range [e, f] and n be number of real solutions of h(x)=14, then (n+e+2f) is

A

8

B

9

C

10

D

11

Text Solution
Verified by Experts

The correct Answer is:D

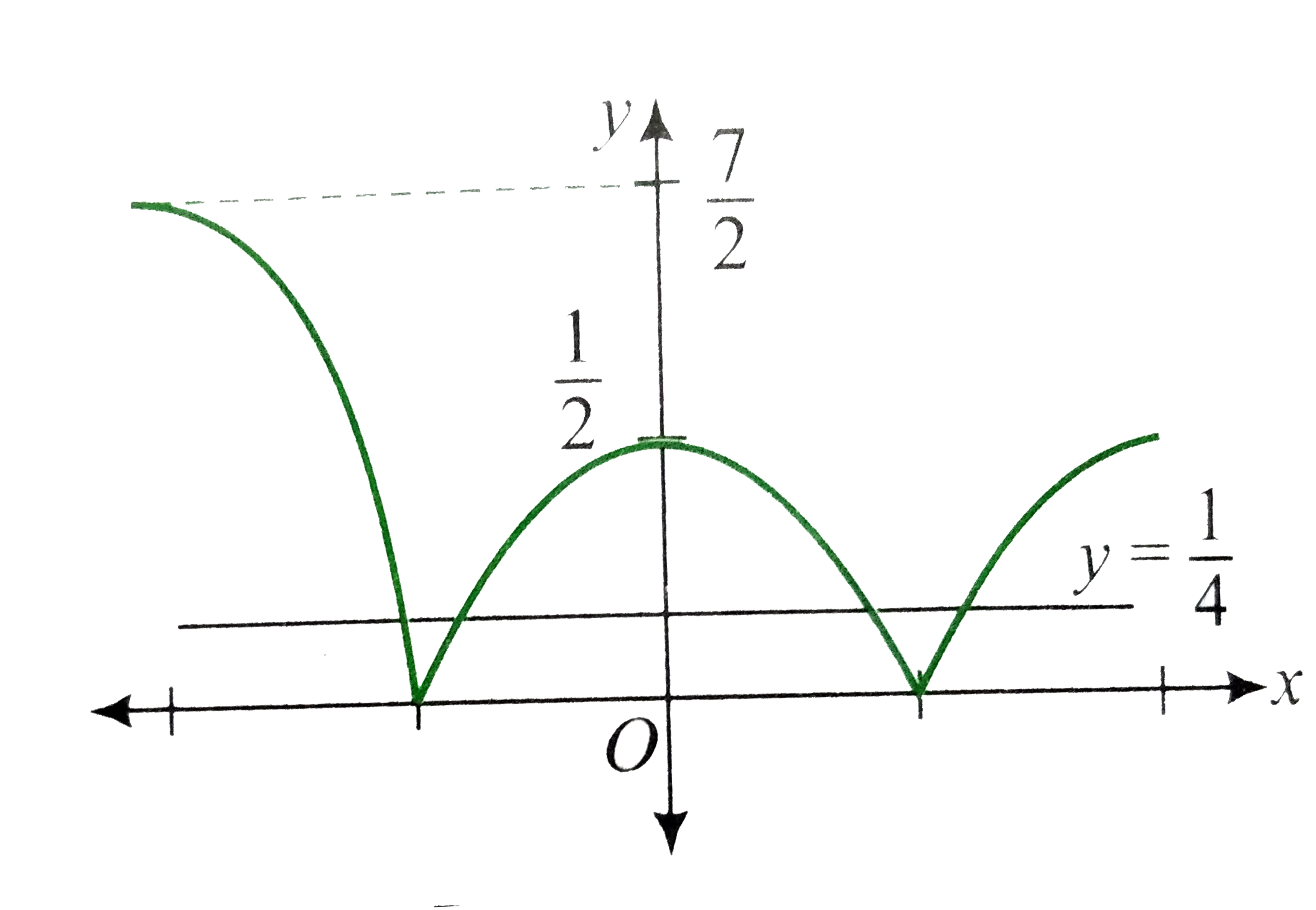
ocr_image
Range of h(x)=[0,72]
Number of solutions of h(x)=14 is n=4.
∴(n+e+2f)=4+0+7=11.

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12MATHSRELATIONS AND FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Consider a function f whose domain is [-3, 4] and range is [-2, 2] with following graph.
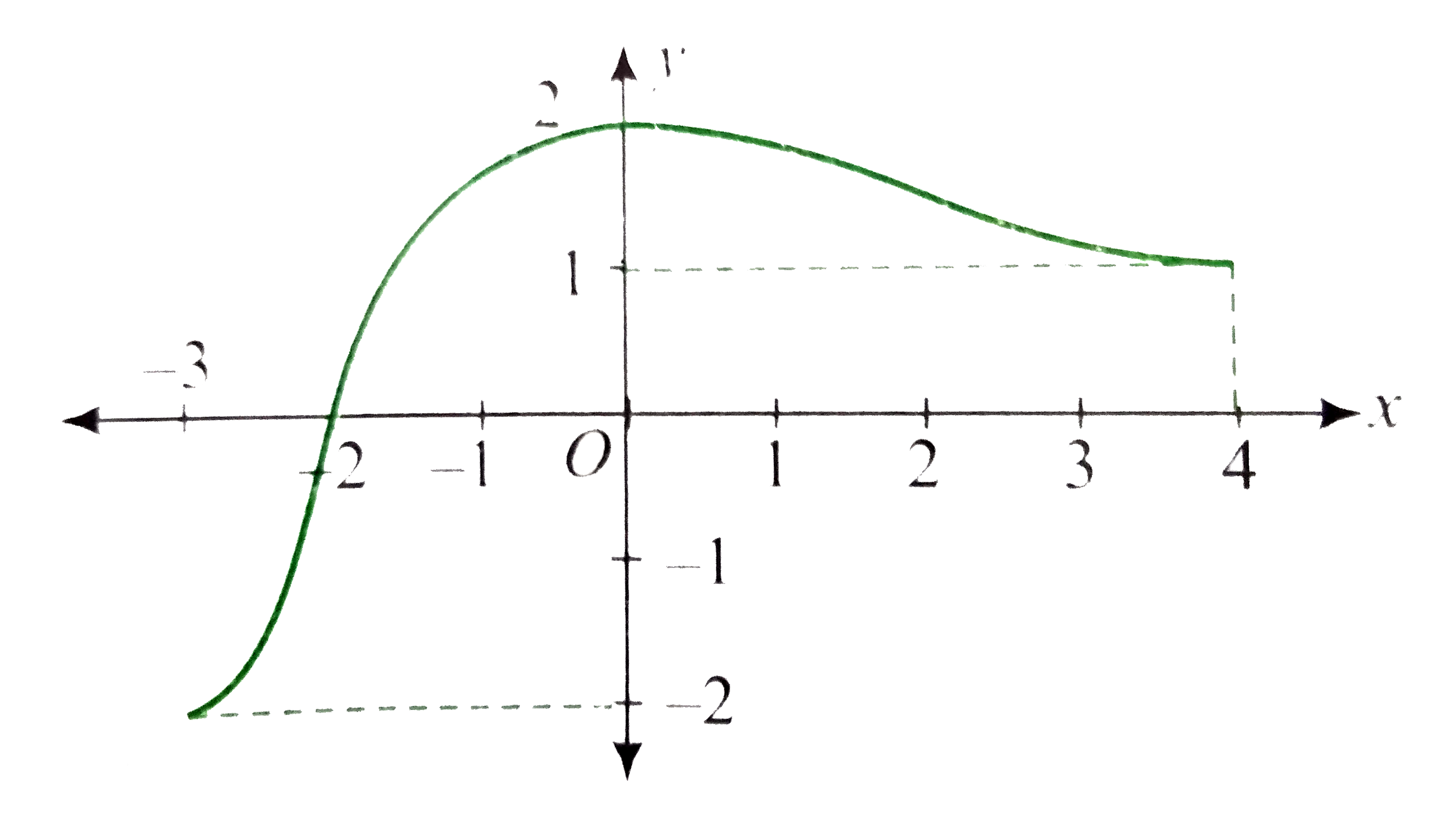
    ocr_image
    Domain and range of g(x)=f(|x|) is [a, b] and [c, d] respectively, then (b−a+c+d) is

    A11
    B10
    C8
    D7

  • If rangr of funtion f(x) whose domain is set of all real numbers is [−2,4], then range of function g(x)=12f(2x+1) is equal to

    A[−2,4]
    B[−1,2]
    C[−3,9]
    D[−2,2]