Let C1andC2 be the graphs of the functions y=x2andy=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axes, meet C2andC3 at Q and R, respectively (see figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
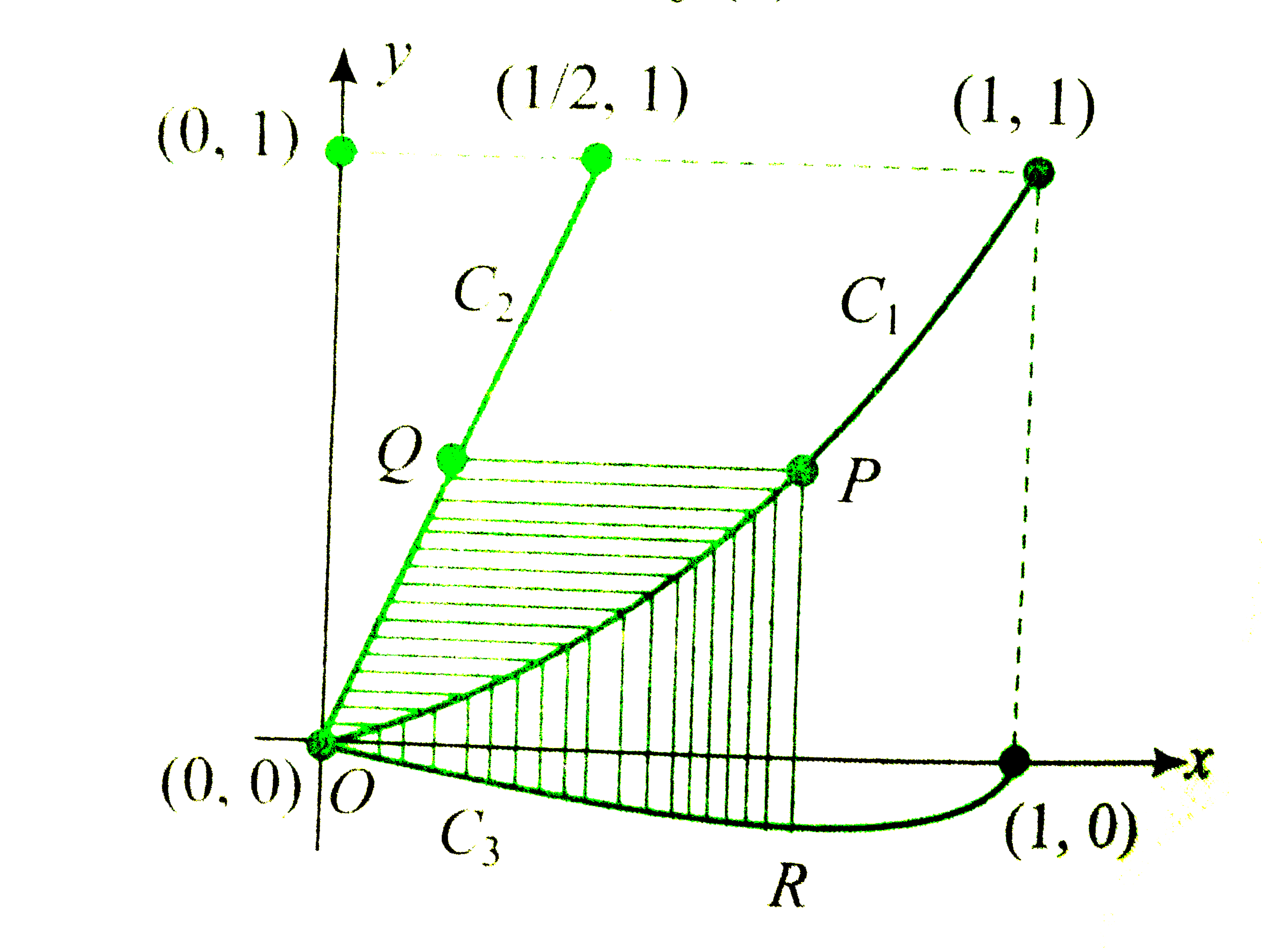
Let P be on C1,y=x2be(t,t2)
∴ y co-ordinate of Q is also t2
Now, Q on y =2x where y=t2
∴ x=t2/2
∴ Q(t22,t2)
For point R, x=t and it is on y=f(x)
∴ R(t,f(t))
Given that,
Area OPQ = Area OPR
⇒ ∫t20(√y−y2)dy=∫t0(x2−f(x))dx
Differentiating both sides w.r.t. t, we get
(√t2−t22)(2t)=t2−f(t)
⇒ f(t)=t3−t2
⇒ f(x)=x3−x2
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.19videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.214videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank29videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank20videos
AREA UNDER CURVES
Similar Questions
Let C1C2 be the graphs of the functions y=x2 and y=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axis, meet C2 and C3 at Q and R, respectively (see Figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x)
View SolutionLet C1andC2, be the graph of the functions y=x2andy=2x,0≤x≤1 respectively. Let C3, be the graph of a function y−(fx),0≤x≤1,f(0)=0. For a point Pand C2, let the lines through P, parallel to the axes, meet C2andC3, at Q and R respectively. If for every position of P (on C1), the areas of the shaded regions OPQandORP are equal, determine the function f(x).
View Solution
Knowledge Check
- Question 1 - Select One
Let C1andC2 be the centres of the circles x2+y2−2x−2y−2=0andx2+y2−6x+14=0 respectively. If P and Q are the points of intersection of these circles, then the area (in sq. units) of the quadrilateral PC1QC2 is:
A8B6C9D4 - Question 2 - Select One
Let C1andC2 be the circles x2+y2−2x−2y−2=0 and x2+y2−6x−6y+14=0 respectively. If P and Q are points of intersection of these circles, then the area (in sq. units ) of the quadrilateral PC1QC2 is :
A4B9C6D8 - Question 3 - Select One
For a > 0, let the curves C1:y2=ax and C2:x2=ay intersect at origin O and a point P. Let the line x=b(0<b<a) intersect the chord OP and the x-axis at points Q and R, respectively. If the line x = b bisects the area bounded by the curves, C1 and C2, and the area of △OQR=1/2, then 'a' satisfies the equation:
Ax6−12x3+4=0Bx6−12x3−4=0Cx6+6x3−4=0Dx6−6x2+4=0
Let C be the centroid of the triangle with vertices (3, -1) (1, 3) and ( 2, 4). Let P be the point of intersection of the lines x+3y−1=0 and 3x−y+1=0. Then the line passing through the points C and P also passes through the point :
View SolutionLet C be the entroid of the triangle with vertices (3, -1) and ( 2, 4). Let P be the point of intersection of the lines x+3y−1=0 and 3x−y+1=0. Then the line passing through the points C and P also passes through the poing :
View SolutionLet C1 and C2 be the centres of the circles
ω1:x2−2x+y2=0
ω2:x2+y2+4x+7y+16=0
respectively. The line joining C1 and C2 intersects the circle ω1 and ω2 at Q and P respectively. If (p,q) is the centre of the circle drawn on PQ as a diameter, then find qpView SolutionLet C1 and C2 be two circles whose equations are x2+y2−2x=0 and x2+y2+2x=0 and P(λ,λ) is a variable point
View SolutionLet C1 and C2 be parabolas x2=y−1 and y2=x−1 respectively. Let P be any point on C1 and Q be any point C2. Let P1 and Q1 be the reflection of P and Q, respectively w.r.t the line y = x then prove that P1 lies on C2 and Q1 lies on C1 and PQ≥[PP1,QQ1]. Hence or otherwise , determine points P0 and Q0 on the parabolas C1 and C2 respectively such that P0Q0≤PQ for all pairs of points (P,Q) with P on C1 and Q on C2
View Solution

