Pair of lines through (1,1) and making equal angle with 3x−4y=1 and 12x+9y=1 intersect x-axis at P1 and P2 , then P1,P2 may be
(87,0) and (97,0)
(67,0) and (8,0)
(87,0) and (18,0)
(8,0) and (18,0)
The correct Answer is:B
Lines making equal angle with given two lines are always parallel to angle bisectors
Equation of angle bisectors 3x−4y−15=12x+9y−115
So bisectors have slope 7,−17
Equation of required lines y−1=7(x−1) and y−1=−17(x−1) which intersect x-axis at (67,0) and (8,0).
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Comprehension Type3videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - STATISTICSEXERCISE - JEE Previous Year10videos
STATISTICS
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year4videos
STRAIGHT LINES
Similar Questions
The straight line passing through P(x1,y1) and making an angle α with x-axis intersects Ax+By+C=0 in Q then PQ=
View SolutionLet P1:2x+y−z=3 and P2:x+2y+z=2 be two planes. Then, which of the following statement(s) is (are) TRUE? The line of intersection of P1 and P2 has direction ratios 1, 2, −1 (b) The line 3x−49=1−3y9=z3 is perpendicular to the line of intersection of P1 and P2 (c) The acute angle between P1 and P2 is 60o (d) If P3 is the plane passing through the point (4, 2, −2) and perpendicular to the line of intersection of P1 and P2 , then the distance of the point (2, 1, 1) from the plane P3 is 2√3
View Solution
Knowledge Check
- Question 1 - Select One
P1:x+3y−z=0andP2:y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2

The angle between P1andP2 is ________.Acos−1(15)Bcos−1(1√55)Ccos−1(2√11)Dcos−1(3√11) - Question 2 - Select One
If the line passing through P(1,2) making an angle 45∘ with the x-axis in the positive direction meets the pair of lines x2+4xy+y2=0 at A and B then PA.PB=
A13/3B13/6C11/6D11/3 - Question 3 - Select One
P1:x+3y−z=0andP2,y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2
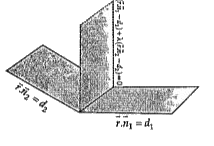
Equation of P3 isA4x + y - 2z = 10Bx + y - 2z = 3Cx + 9y + 11z = 0D4x - y + z = 0
If the line passing through P(1,2) making an angle of 450 with the x-axis in the positive direction meets the pair of lines x2+4xy+y2=0 at A and B then PA:PB=
View SolutionA line through point A(1,3) and parallel to the line x-y+1 = 0 meets the line 2x-3y + 9 = 0 at point P. Find distance AP without finding point P.
View SolutionFind an equation for the plane through P0=(1,0,1) and passing through the line of intersection
of the planes x+y−2z=1andx+3y−z=4.View SolutionP1:x+3y−z=0andP2:y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2
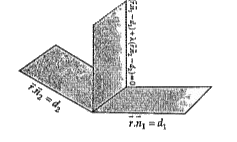
__________ is a point on P3.View SolutionP1:x+3y−z=0andP2:y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2
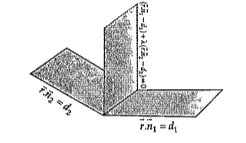
Distance of P3 from origin is _______ units.View Solution

