A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle. Show that the maximum length of the hypotenuse is ${(a^{\frac{2}{3}} + b^{\frac{2}{3}})}^{\frac{3}{2}}$ .

Video Solution

Text Solution

Verified by Experts

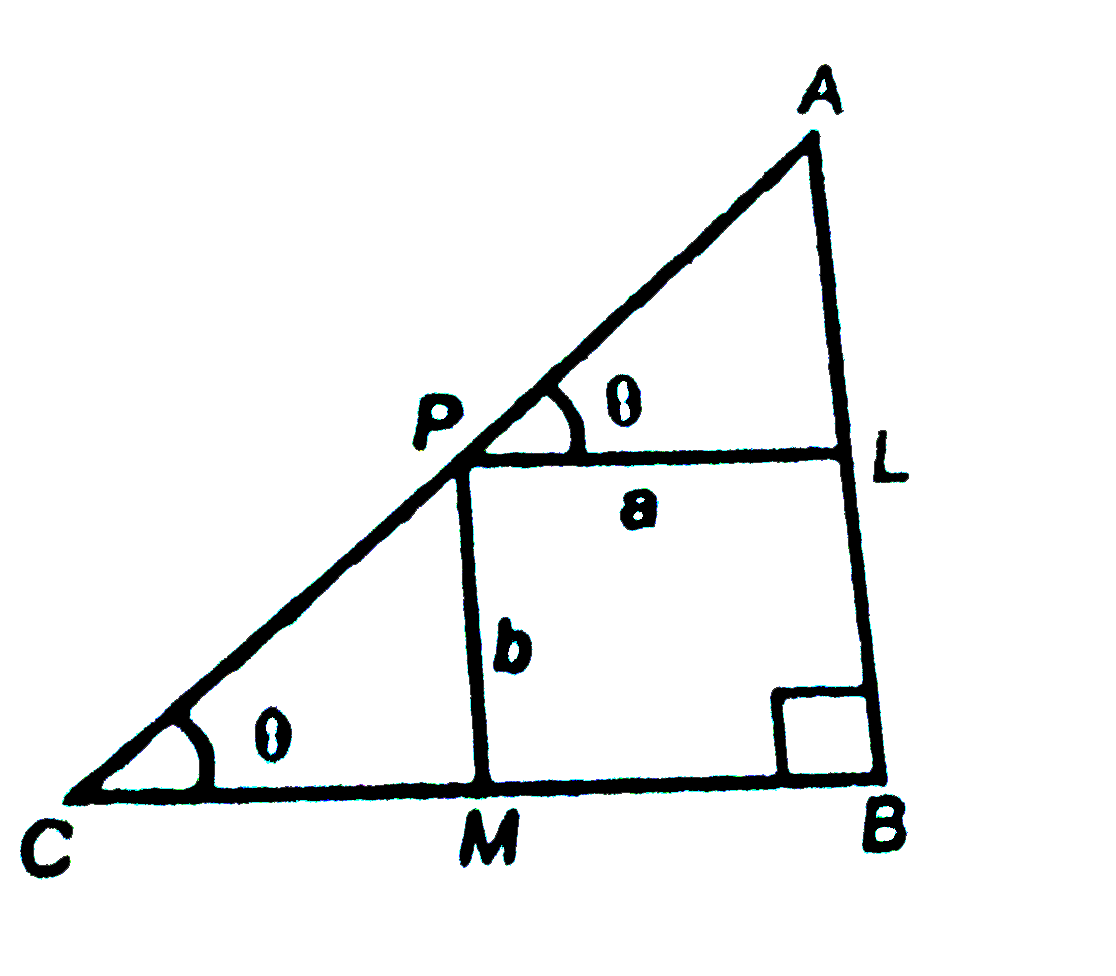
Let a point P on the hypotenuse AC of a right $Δ A B C$ such that
$P L ⊥ A B = a and P M ⊥ B C = b$ Again, let
$∠ A P L = ∠ A C B = θ$ then,
$A p = a sec θ, P C = b cos e c θ$
Again if the length of hypotenuse is l, then $l = A P + P C \Rightarrow l = a sec θ + b cos e c θ, 0 < θ < \frac{π}{2}$
Differentiate w.r.t. $θ$ ,
$\frac{d l}{d θ} = a sec θ tan θ - b cos e c θ cot θ$
For maxima/minima, $\frac{d l}{d θ} = 0$
$\Rightarrow a sec θ tan θ = b cos e c θ cot θ$
$\Rightarrow \frac{a sin θ}{{cos}^{2} θ} = \frac{b cos θ}{{sin}^{2} θ} \Rightarrow \frac{{sin}^{3} θ}{{cos}^{3} θ} = \frac{b}{a}$
$\Rightarrow r {tan}^{3} θ = \frac{b}{a} \Rightarrow tan θ = {(\frac{b}{a})}^{\frac{1}{3}}$
Now $\frac{d^{2} l}{d θ^{2}} = a (sec θ \times {sec}^{2} θ + tan θ \times sec θ t e n θ)$
$- b [cos e c θ (- cos e c^{2} θ) + cot θ (- cos e c θ cot θ)]$
$= a sec θ ({sec}^{2} θ + {tan}^{2} θ) + b cos e c θ (cos e c^{2} θ + {cot}^{2} θ)$
since $0 < θ < \frac{π}{2}$ so the trigonometric ratios will be positive and $a > 0, b > 0$
$∴ \frac{d^{2} l}{d θ^{2}} > 0$
$\Rightarrow when tan θ = {(\frac{b}{a})}^{\frac{1}{3}}$

then l is minimum,
$∴$ minimum value of
$l = a sec θ + b cos e c θ$
$a \frac{\sqrt{a^{\frac{2}{3}} + b^{\frac{2}{3}}}}{a^{\frac{1}{3}}} + b \frac{\sqrt{a^{\frac{2}{3}} + b^{\frac{2}{3}}}}{b^{\frac{1}{3}}}$
$= \sqrt{a^{\frac{2}{3}} + b^{\frac{2}{3}}} (a^{\frac{2}{3}} + b^{\frac{2}{3}}) = {(a^{\frac{2}{3}} + b^{\frac{2}{3}})}^{\frac{3}{2}}$ .

Updated on:21/07/2023

Altitude and base of a right angle triangle are (x+2) and (2x+3) ( in cm ). If the area of the triangle be 60 $c m^{2}$ , the length of the hypotenuse is :
A21 cm
B13 cm
C17 cm
D15 cm
Altitude and base of a right angle triangle are (x+2) and (2x+3) ( in cm ). If the area of the triangle be 60 $c m^{2}$ , the length of the hypotenuse is :
A21 cm
B13 cm
C17 cm
D15 cm