Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is $\frac{2 R}{\sqrt{3}}$ . Also find the maximum volume.

Video Solution

Text Solution

Verified by Experts

Let 'r' be the radius and 'h' be the height of the cylinder.
$∴ {(2 r)}^{2} + h^{2} = {(2 R)}^{2}$

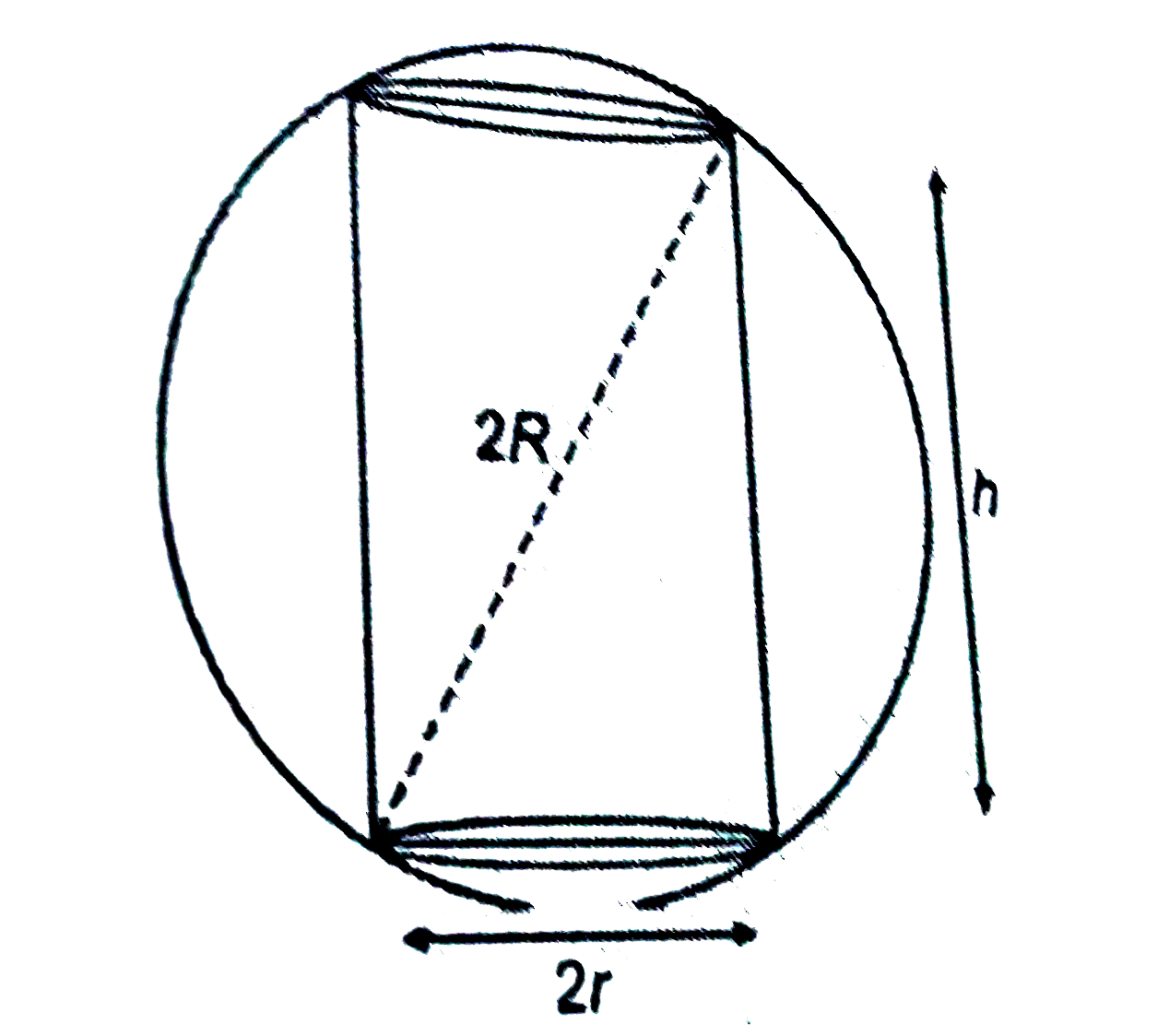
$\Rightarrow r^{2} = R^{2} - \frac{h^{2}}{4}$ ….(1)
Volume of cylinder
$V = π r^{2} h = π (R^{2} - \frac{h^{2}}{4}) h$
$= π (R^{2} h - \frac{h^{3}}{4})$
$\Rightarrow \frac{d V}{d h} = π (R^{2} - \frac{3 h^{2}}{4})$ [From eqn. (1)]
For maxima/minima $\frac{d V}{d h} = 0$
$\Rightarrow R^{2} - \frac{3 h^{2}}{4} = 0 \Rightarrow h = \frac{2 R}{\sqrt{3}}$
Now $\frac{d^{2} V}{d h^{2}} = π (- \frac{3 h}{2}) < 0$
$∴ a t h = \frac{2 R}{\sqrt{3}}$ the volume of cylinder is maximum.

Updated on:21/07/2023