Find the points at which the function f given by f(x)=(x−2)4(x+1)3 has local maxima local minima point of inflexion
Given equation is ,
f(x)=(x−2)4(x+1)3
f'(x)=(x−2)43(x+1)2+(x+1)34(x−2)3
=(x−2)3(x+1)2{3(x−2)+4(x+1)}
=(x−2)3(x+1)2(7x−2)
For maxima/minima, f'(x)=0
⇒(x−2)3(x+1)2(7x−2)=0
⇒x=2,−1,27
(i) At x=27,
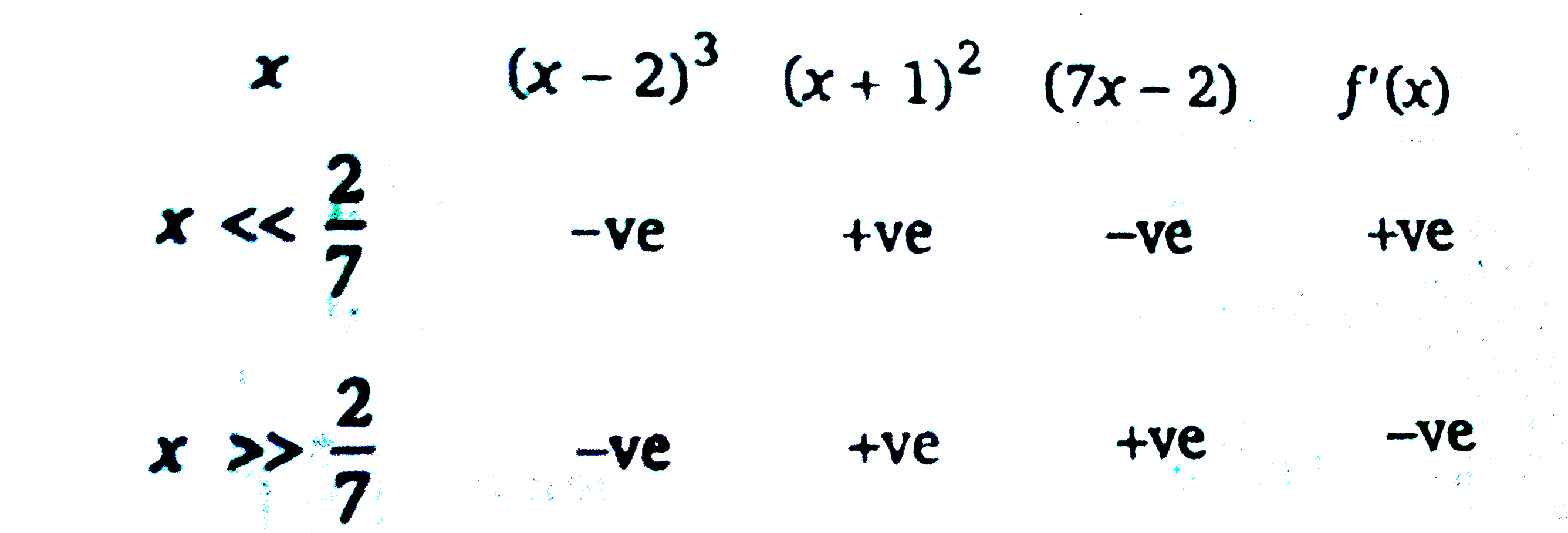
∴f'(x) changes its sign from positive to negative, so x=27 is a point of local maxima.
(ii) At x = 2,
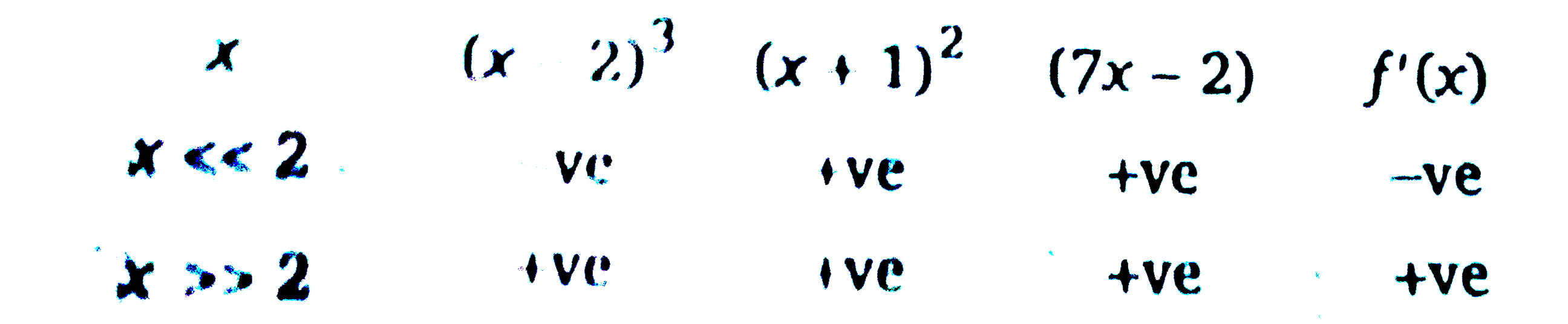
∴f'(x) changes its sign from negative to positive, so x = 2 is a point of local minima.
(iii) At x =- 1,
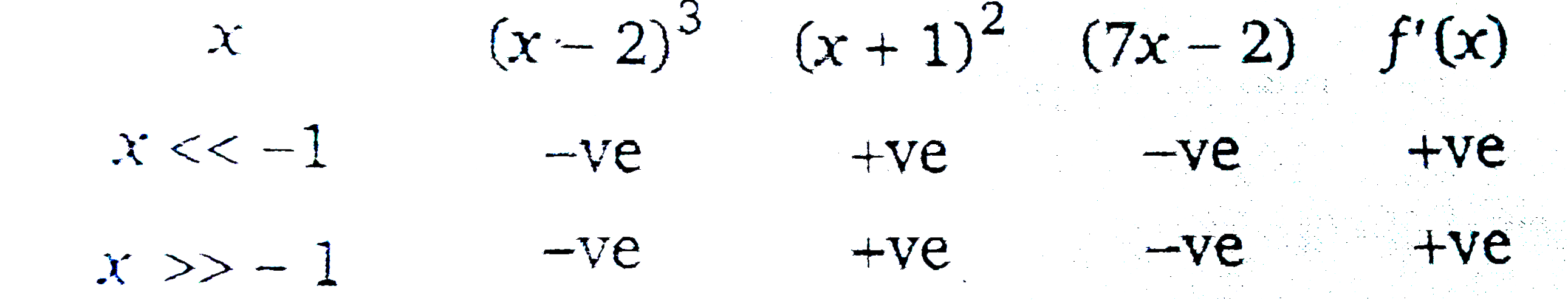
∴f'(x) does not change its sign , so = - 1 is a point of inflexion.
Topper's Solved these Questions
Similar Questions
Find the points at which the function f given by f(x)=(x−2)4(x+1)3 has local maxima and local minima and points of inflexion.
View SolutionFind the points of local maxima and minima of the function f(x)=x2−4x.
View SolutionFind the points of local maxima and minima of the function f given by f(x)=x3−12x2+36x+5 .
View SolutionFor the function f(x)=43x3−8x2+16x+5,x=2 is a point of local maxima (2) local minima point of inflexion (4) decreasing increasing
View SolutionFind all points of local maxima and local minima of the function f given byf(x)=x3−3x+3.
View SolutionFind the local maxima and minima of the function f(x)=x3−2x2+x+6.
View SolutionFind the points of local maxima/minima of function
f(x)=xlnxView SolutionFind the points of local maxima/minima of function
f(x)=−(x−1)3(x+1)2View SolutionFind all the points of local maxima and minima of the function f given by f(x)=sinx−cosx,x∈[0,2π]
View SolutionFind all the points of local maxima and minima of the function f given by f(x)=4x3−12x2+12x+10
View Solution

