The momentum of a particle moving in straight line is given by
p=t+1t(in m/s)
find the (time t>0) at which the net force aciting on particle is 0 and it's momentum at that time.
1kgm/sec
2kgm/sec
3kgm/sec
4kgm/sec
The correct Answer is:B
To solve the problem step by step, we will follow the outlined process:
1. Given Momentum Expression:
The momentum p of the particle is given by the equation:
p=t+1t
2. Finding the Force:
The force acting on the particle can be found by differentiating the momentum with respect to time t. The formula for force F is given by:
F=dpdt
We differentiate p:
dpdt=ddt(t+1t)
Using the rules of differentiation:
- The derivative of t is 1.
- The derivative of 1t is −1t2.
Therefore, we have:
dpdt=1−1t2
3. Setting Force to Zero:
To find the time at which the net force is zero, we set the derivative equal to zero:
1−1t2=0
Rearranging gives:
1t2=1
Taking the reciprocal:
t2=1
Thus, we find:
t=±1
Since time must be greater than zero, we take:
t=1 second
4. Finding the Momentum at that Time:
Now we substitute t=1 back into the momentum equation to find the momentum at that time:
p=1+11=1+1=2 kg m/s
5. Final Answers:
- The time at which the net force acting on the particle is zero is t=1 second.
- The momentum at that time is p=2 kg m/s.
Summary of the Solution:
- The time t at which the net force is zero is 1 second.
- The momentum at that time is 2 kg m/s.
The momentum p of the particle is given by the equation:
p=t+1t
The force acting on the particle can be found by differentiating the momentum with respect to time t. The formula for force F is given by:
F=dpdt
We differentiate p:
dpdt=ddt(t+1t)
Using the rules of differentiation:
- The derivative of t is 1.
- The derivative of 1t is −1t2.
dpdt=1−1t2
To find the time at which the net force is zero, we set the derivative equal to zero:
1−1t2=0
Rearranging gives:
1t2=1
Taking the reciprocal:
t2=1
Thus, we find:
t=±1
Since time must be greater than zero, we take:
t=1 second
Now we substitute t=1 back into the momentum equation to find the momentum at that time:
p=1+11=1+1=2 kg m/s
- The time at which the net force acting on the particle is zero is t=1 second.
- The momentum at that time is p=2 kg m/s.
- The time t at which the net force is zero is 1 second.
- The momentum at that time is 2 kg m/s.
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY133videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHEMATICS58videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION - 2 [MULTIPLE CORRECT CHOICE TYPE]6videos
TEST PAPERS
- BOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions1videos
PROBABILITY
- BOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column7videos
THERMODYNAMICS
Similar Questions
The speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View SolutionThe displacement of a particle moving in straight line is given as function of time as s=(t33−3t22+2t),s is in m and t is in sec. The particle comes to momentary rest n times Find the value of n
View Solution
Knowledge Check
- Question 1 - Select One
The position of a particle moving on a straight line depends on time t as
x=(t+3)sin(2t)AIts velocity at the initial moment is 6 m/sBIts acceleration at the initial is −8m/s2CIt has velocity of 3 m/s at t=π2 secDIt has an acceleration of 2m/s2 at t=π4 sec - Question 2 - Select One or More
Kinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
ADirectly proportional to the speed of the particleBInversely proportional to √tCInversely proportional to the speed of the particleDDirectly proportional to √t - Question 3 - Select One
The momentum of a moving particle given by p=tlnt. Net force acting on this particle is defined by equation F=dpdt. The net force acting on the particle is zero at time
At=0Bt=1eCt=1e2DNone of these
The space s described in time t by a particle moving in a straight line is given by s=t5−40t3+30t2+80t−250 . Find the minimum value of acceleration.
View SolutionThe velocity-time graph of a particle moving in a straight line is shown in figure. The mass of the particle is 2kg. Work done by all the forces acting on the particle in time interval between t=0 to t=10s is
 View Solution
View SolutionKinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
View SolutionMomentum of a body moving in a straight line is p=(2t3+t2+2t+1)kg m/s. Force acting on a body at t=2 sec.
View SolutionVelocity-time graph of a particle moving in a straight line is shown in the figure. Mass of the particle is 2 kg. Work done by all the forces acting on the particle in time interval t = 0 to t = 10 sec is
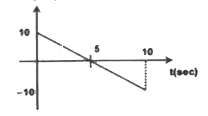 View Solution
View Solution

