The spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
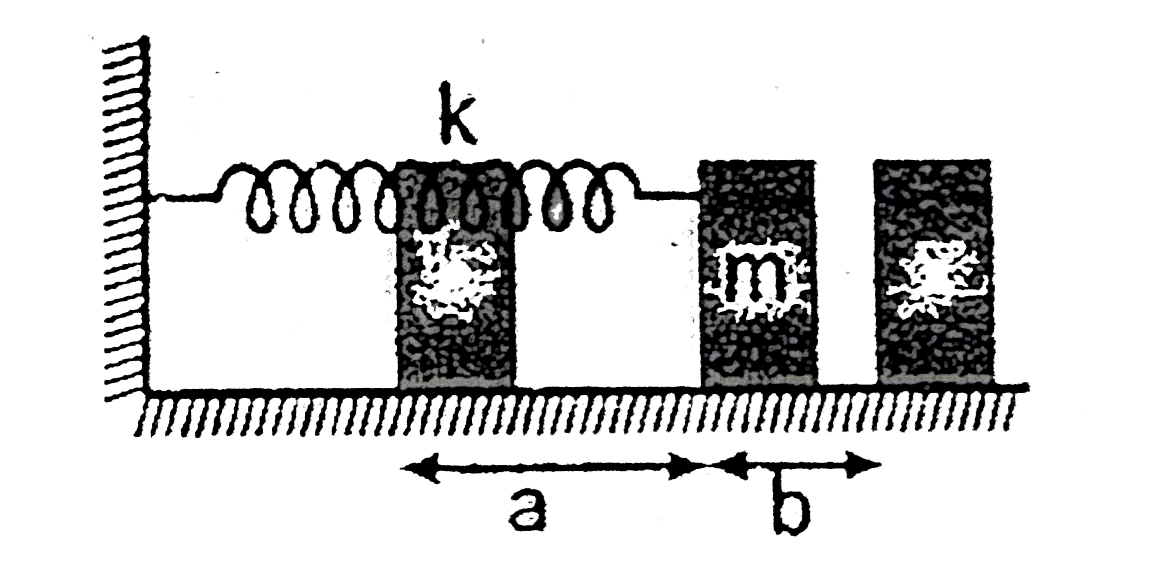
work done by the spring on the block =12k(a−b)2
work done by the spring on the block =12k(a2+b2)
coefficient of friction =k(a−b)2mg
coefficient of friction =k(a+b)2mg
The correct Answer is:C
Step by step video & image solution for The spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
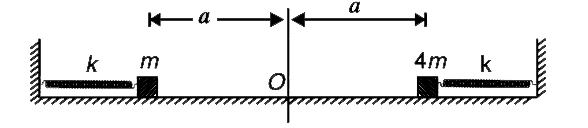
Two small blocks of mass m and 4m are connected to two springs as shown in fig. Both springs have stiffness K and they are in their natural length when the blocks are at point O. Both the blocks are pushed so that both the springs get compressed by a distance a. First the block of mass m is released and after it travels through a distance(1−√32)
the second block is also released.
(a) At what distance from point O will the two blocks collide?
(b) How much time the two blocks need to collide after the block of mass 4m is released?
View SolutionFor the system shown in fig., initially the spring is compressed by a distance 'a' from its natural length and when released, it moves to a distance 'b' from its equillibrium position, the decrease in amplitude for half cycle (-a to +b) is :

View Solution
Knowledge Check
A block of mass m is pushed up against a spring, compressing it a distance x, and the block is then released. The spring projects the block along a frictionaless horizontal surface, grving the block a speed v. The same spring projects a second block of mass 4m, giving it a speed 3v. What distance was the spring compressed in the second case ?
A6xBx6C36xD12xTwo trolleys of mass m and 3m are attached by a spring. The spring was compressed and then released , they move off in opposite direction and comes to rest after covering distances s1 and s2 respectively. Assuming the coefficient of friction to be uniform , the ratio of distances s1:s2 is
A1:9B1:3C3:1D9:1A block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released, the period of oscillation of the block for a complete cycle is equal to
 A4π3√mkBπ√2√mkC2π3√mkDNone of these
A4π3√mkBπ√2√mkC2π3√mkDNone of these
In the figure shown the spring is compressed by 'x0' and released . Two block 'A' and 'B' of masses 'm' and '2m' respectively are attached at the ends of the spring. Blocks are kept on a smooth horizontal surface and released. Find the work done by the spring on 'A' by the time compression of the spring reduced to x02.

View SolutionIn figure a spring with k=168N/m is in its relaxed length and is at the top of a frictionless incline of angle θ=37∘. The lower end of the incline is at distance D = 1 m from the end of the spring. A small blcok of mass 2 kg is pushed against the spring until the spring is compressed by 0.2 m and released from rest.
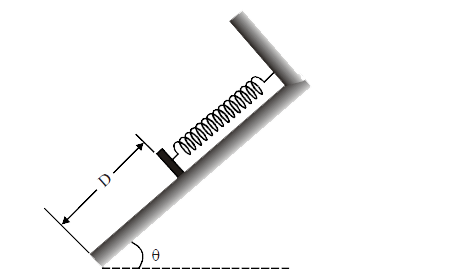
What is the speed of the block at the instant the spring returns to its relaxed length (which is when the block loses contact with the spring)?
View SolutionFor the arrangement shown in figure, the spring is inilially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m

View SolutionFor the arrangement shown in figure, the spring is initially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

(a) If the coefficient of restitution is 1√2 , find the maximum compression in the spring after collision.
(b) If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
View Solution
