If $f (x) = sin x + | sin x | and g (x) = f (x - π) + f (x + 2 π)$ , then value of $5 π f - 2 π g (x) d x$ is

A

15

B

7

C

12

D

28

Text Solution

Verified by Experts

The correct Answer is:A

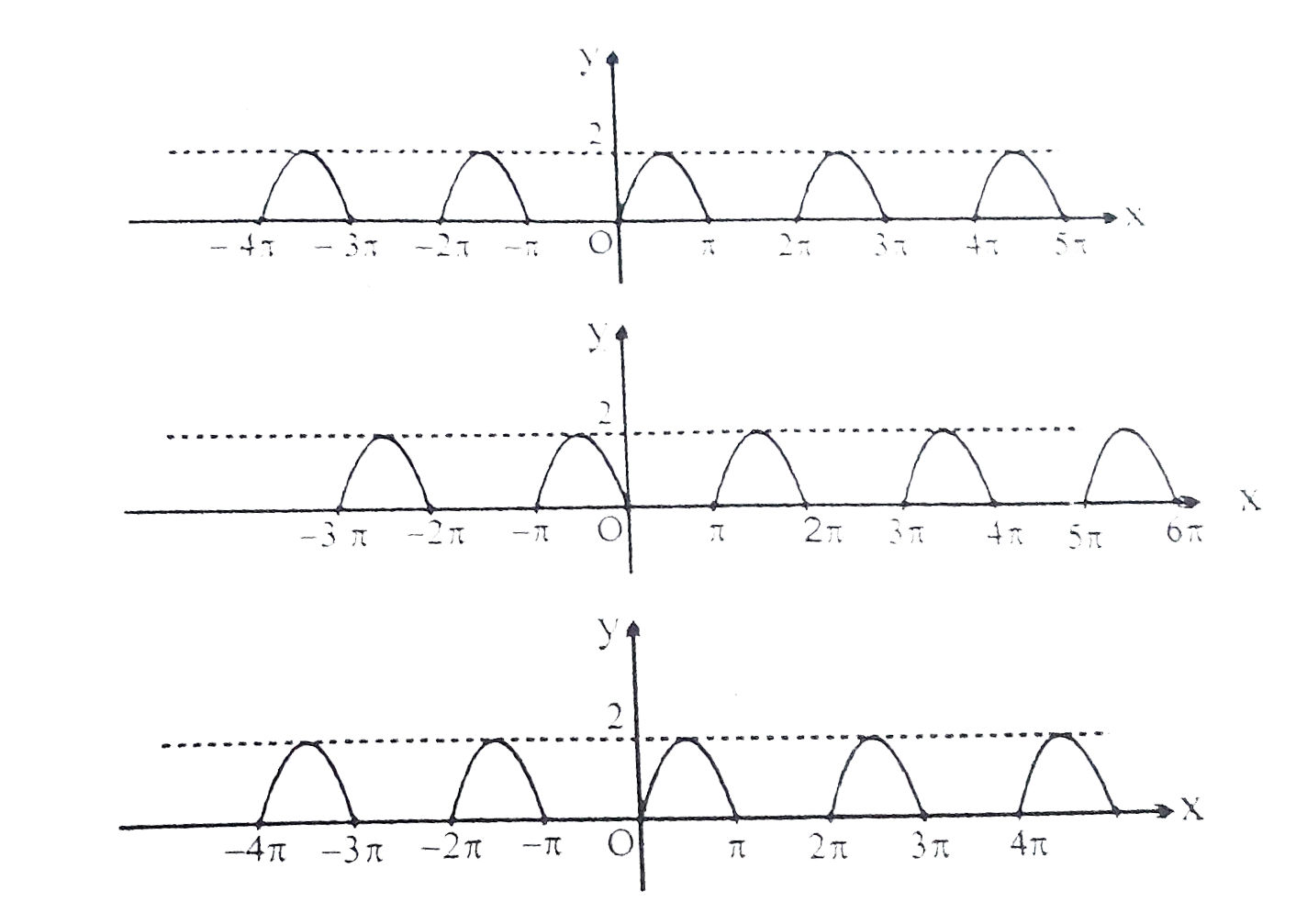
$∴ g (x) = f (x - π) + f (x + 2 π)$

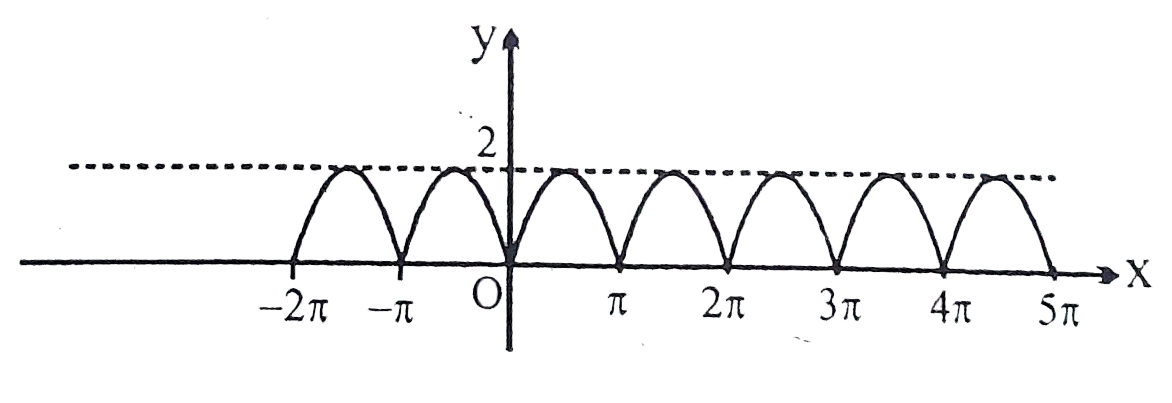
$5 π f - 2 π g (x) d x$
$∴ required area = 2 [2 \times 7] = 28$ .
Aliter : $g (x) = f (x - π) + f (x + 2 π) = (- sin x + | sin x |) + (sin x | sin x |) \Rightarrow g (x) = 2 | sin x |$
$So, 5 π f - 2 π g (x) d x = 28$ .

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If f(x) = 2 sinx, $g (x) = {cos}^{2} x$ , then the value of $(f + g) (\frac{π}{3})$
A1
B $\frac{2 \sqrt{3} + 1}{4}$
C $\sqrt{3} + \frac{1}{4}$
D0
Question 2 - Select One
$f (x) = sin x + \int_{- π / 2}^{π / 2} (sin x + t cos x) f (t) d t$
The value of $\int_{0}^{π / 2} f (x) d x$ is
A $1$
B $- 2$
C $- 1$
D $2$
Question 3 - Select One
If $f (x) + f (π - x) = 1$ and $g (x) + g (π - x) = 1$ , then : $\int_{0}^{π} [f (x) + g (x)] d x =$
A $\frac{3 π}{2}$
B $\frac{π}{2}$
C $2 π$
D $π$

BANSAL-TEST PAPERS-MATHS SECTION-3 PART-A [SINGLE CORRECT CHOICE TYPE]

Home
Ask Doubt
Profile