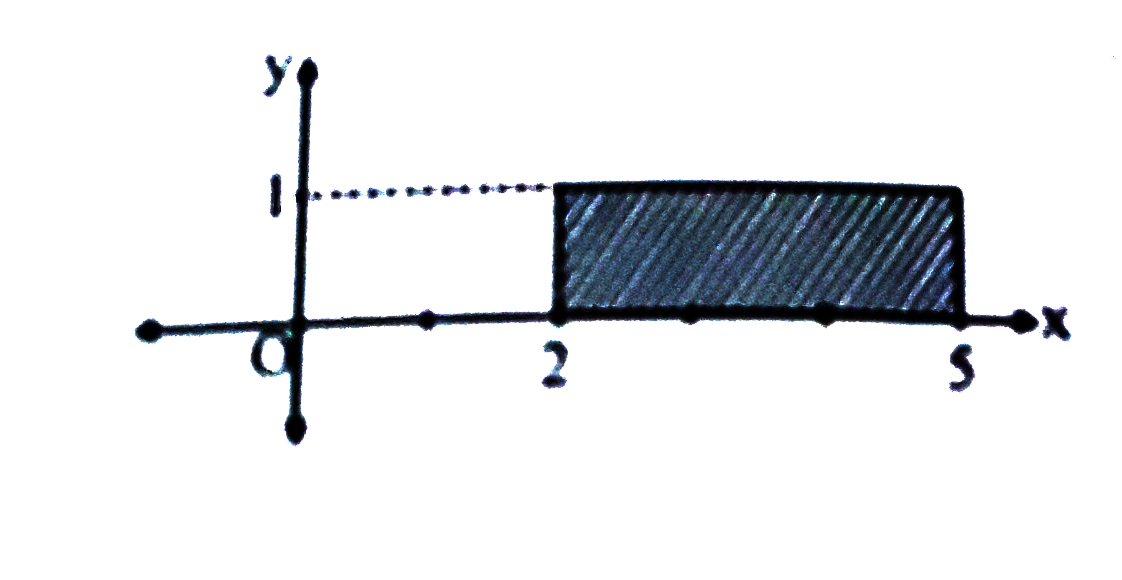
Suppose f:R→R be a continuous function such that f(3x)=f(x)∀x∈R. IF f(2) = 5, then 5f2sgn(f(x))dx equals
[Note : sign k denotes signum function of k.]
2
9
6
3
The correct Answer is:A
f(3x)=f(x)=f(x3)=.......=f(x3n)
Taking limit n→∞,f(3x)=f(0)
∴ f(x) is a contant function.
∴ f(x)=5∀x∈R(As,f(2)=5)
∴ sng(f(x))=1
∴ 5f2sgn(f(x))dx=3×1=3.
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION-3 PART-B [MULTIPLE CORRECT CHOICE TYPE]
5 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION-3 PART-C [INTEGER TYPE]
5 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY SECTION-2 PART-C [INTEGER TYPE]
5 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Video
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
Knowledge Check
Let f:R→R be a function such that f(x)=x3+x2f'(1)+xf(2)+f(3),ξnR. Then f(2) equals:
A30B8C2D−4Let f : R → R be a continuous function satisfying
f(x)+xf0tf(t)dt+x2=0
for all x∈R. Then-Alim.x→−∞f(x)=2Blim.x→−∞f(x)=−2Cf(x) has more than one point in common with x-axisDf(x) is an odd functionsIf for a continuous function f, ∫a−af(x)dx=K∫a0(f(x)+f(−x)) dx then the value of K is
A1B1/2C2Da
A continuous real function f satisfies f(2x)=3f(x)∀x∈R.If∫10f(x)dx=1, then find the value of ∫21f(x)dx
View SolutionLet f(x) be a continuous function such that f(a-x)+f(x)=0 for all x∈[0,a]. Then, the value of the integral
a∫011+ef(x)dx is equal to
View SolutionA continuous real function f satisfies f(2x)=3(f(x)∀x∈R.If∫10f(x)dx=1, then find the value of ∫21f(x)dx
View SolutionLet f:[2,5]→[2,5]be a bijective function such that ddxf−1(x)>0∀(x)∈[2,5]then∫52(f(x)+f−1(x))s dx is equal to 7k. then value of k is
View SolutionIf a function is defined such as f(x+k)=f(x) for k∈I+ and I=∫k0f(x)dx , then ∫k2−k0f(x)dx equals to
View Solution
