Consider $f (x) = Lim n \to \infty ({(a^{n} + b^{n})}^{\frac{1}{n}} sin x + {e^{x}}^{n}) ([\frac{1}{n {cot}^{- 1} n}] + 1), \forall x \in R$
where $a > b > 0$ .
[Note : {k} and [k] denotes fractinal part of k and greatest interger less than or equal to k respectively.]
If H(x)=sgn (f(x)-3) has exactly one point of discontinuity $\forall x \in [0, 2 π]$ , then number of integral value of a, is

A

1

B

2

C

0

D

infinite

Text Solution

Verified by Experts

The correct Answer is:A

$f (x) = Lim n \to \infty ⎛ ⎝ ⎛ ⎝ a {(1 + {(\frac{b}{a})}^{n})}^{\frac{1}{n}} ⎞ ⎠ sin x + {e^{x}}^{n} ⎞ ⎠ ([\frac{\frac{1}{n}}{{tan}^{- 1} \frac{1}{n}}] + 1)$
$∴ f (x) = (a sin x + 0) (1 + 1)$
$∴ f (x) = 2 a sin x$
(i) $H (x) = s g n (2 a sin x - 3)$ has exactly one point of discontinuty in $[0, 2 π]$ , then $2 a sin x - 3 = 0$ must have one real root in $[0, 2 π], \frac{sin (3)}{2 a}$
$∴ a = \frac{3}{2}$ only
$∴$ Number integral value of a is zero.
$G (x) = | 2 a sin x | + 2 a sin | x |$
(ii)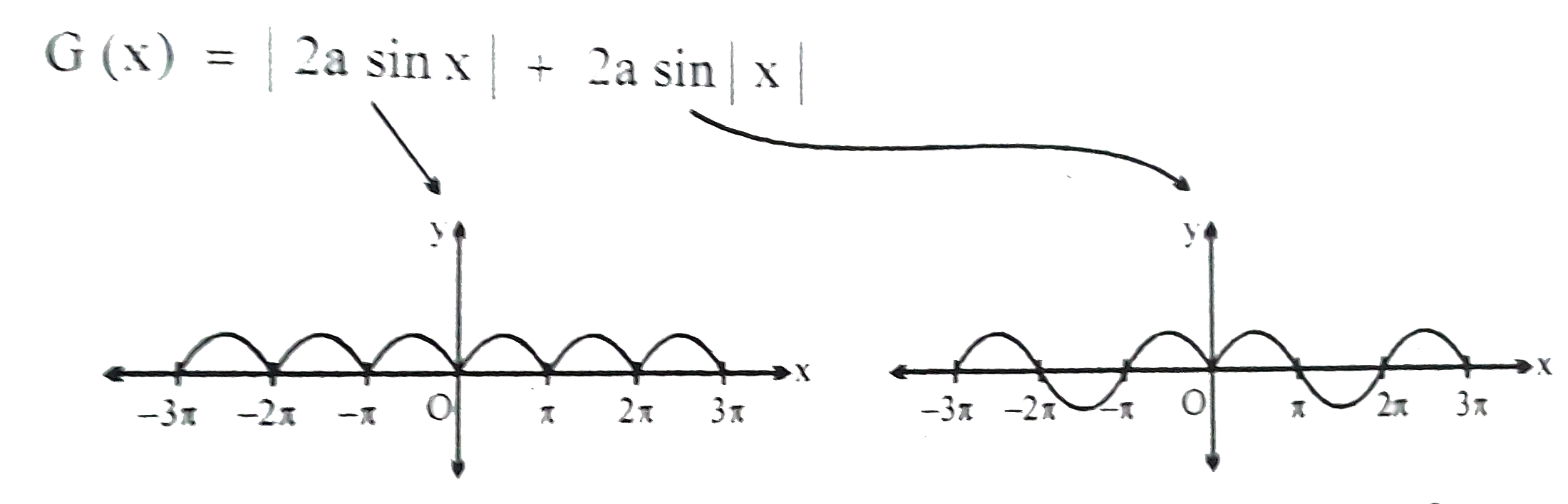
Number of non-differential point of G(x) is $x = - 2 π, - π, 0, π, 2 π$
separately we can prove that G(x) is non-differentiable at x=0.

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Consider $f (x) = Lim n \to \infty ({(a^{n} + b^{n})}^{\frac{1}{n}} sin x + {e^{x}}^{n}) ([\frac{1}{n {cot}^{- 1} n}] + 1), \forall x \in R$
where $a > b > 0$ .
[Note : sgn $α$ denote signum function of $α$ .]
Number of points where $G (x) = | f (x) | + f (| x |)$ is non-differentiable in $(- 3 π, 3 π)$ , is
A6
B5
C4
D7
Question 2 - Select One
If $n \in N$ , and $[x]$ denotes the greatest integer less than or equal to x, then $lim x \to n {(- 1)}^{[x]}$ is equal to.
A1
B-1
C0
Dnone of these
Question 3 - Select One
Let $f (x) = lim n \to \infty \frac{sin x}{1 + {(2 sin x)}^{2 n}}$ then f is discontinuous at
A $π$
B $π / 3$
C $π / 4$
D $π / 6$

BANSAL-TEST PAPERS-MATHS SECTION - 2 PART A [PARAGRAPH TYPE]

Home
Ask Doubt
Profile