Question

Consider $f\left(x\right)=\underset{n\to \infty }{Lim}({(a^n+b^n)}^{\frac{1}{n}}\sin x+{\left\{e^x\right\}}^n)(\left[\frac{1}{n{\cot }^{-1}n}\right]+1),\forall x\in R$
where $a>b>0$.
[Note : sgn $\alpha$ denote signum function of $\alpha$.]
Number of points where $G\left(x\right)=\left|f\left(x\right)\right|+f\left(\left|x\right|\right)$ is non-differentiable in $(-3\pi ,3\pi )$, is

Options

A. 6
B. 5
C. 4
D. 7

Answer

A

Explanation

`f(x)=underset(ntooo)Lim((a(1+((b)/(a))^(n))^((1)/(n)))sinx+{e^(x)}^(n))([((1)/(n))/("tan"^(-1)(1)/(n))]+1)`
`:." "f(x)=(asinx+0)(1+1)`
`:." "f(x)=2asinx`
(i) `H(x)=sgn (2asinx-3)` has exactly one point of discontinuty in `[0,2pi]`, then `2a sinx-3=0` must have one real root in `[0,2pi],sin(3)/(2a)`
`:." "a=(3)/(2)` only
`:." "` Number integral value of a is zero.
`G(x)=|2asinx|+2asin|x|`
(ii)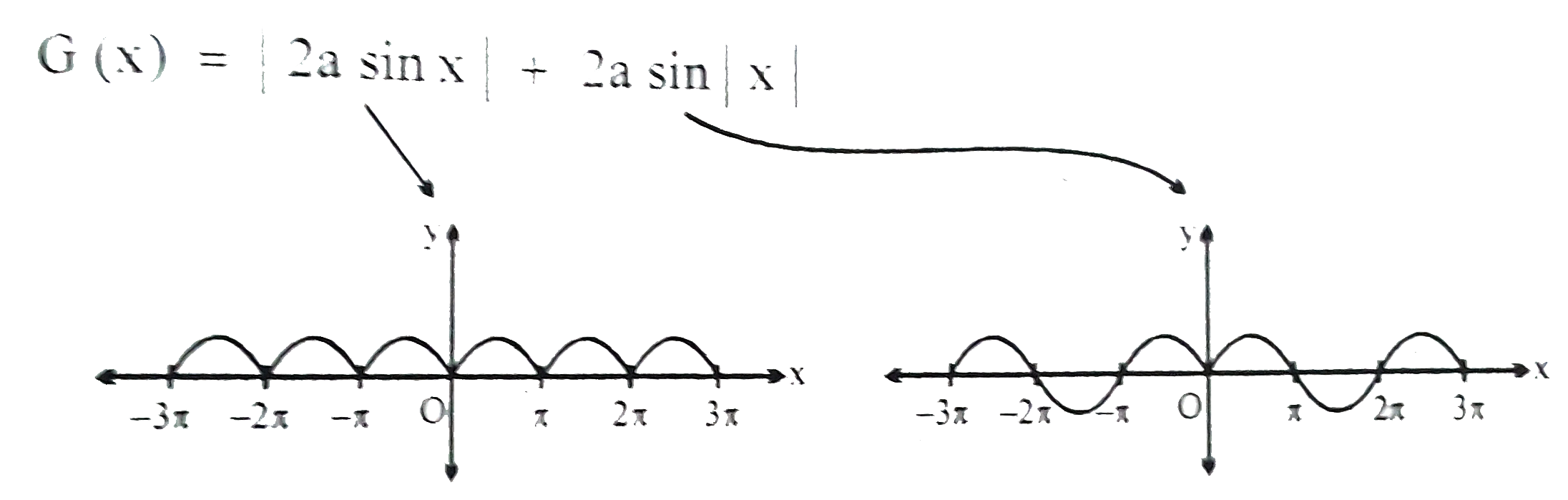
Number of non-differential point of G(x) is `x=-2pi,-pi,0,pi,2pi`
separately we can prove that G(x) is non-differentiable at x=0.