Consider f(x)⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩|[x]|,0≤{x}<12,∀x∈[−72,72]|x|,12≤{x}<1
Number of solution of the equation f(x)=52 is equal to

A

2

B

3

C

4

D

infinite

Text Solution
Verified by Experts

The correct Answer is:A

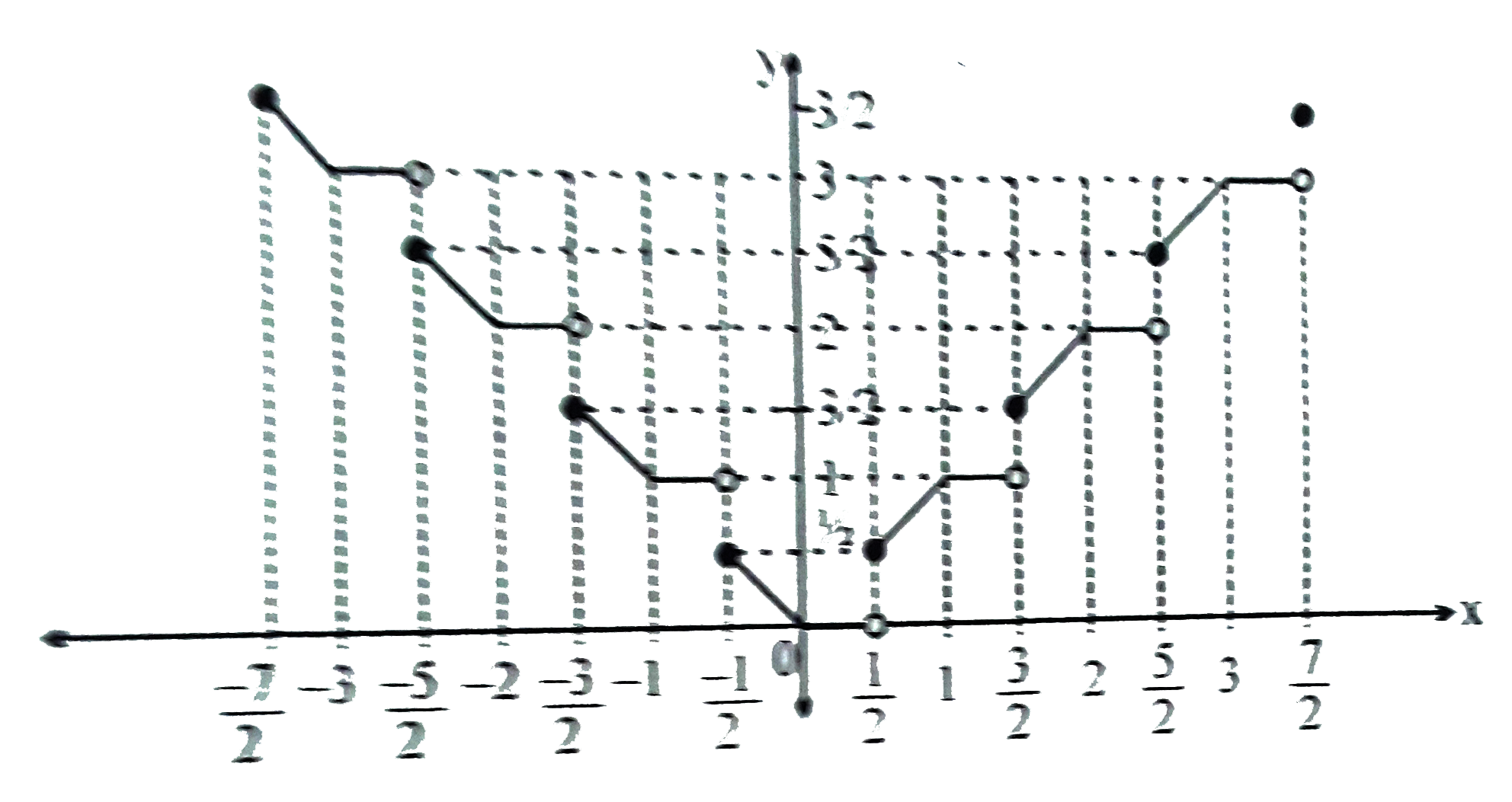
ocr_image
L = Number of point of discontinuous = 7
M = Number of point non-differentiability = 14
Hence (L+M)=21.

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Consider f(x)⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩|[x]|,0≤{x}<12,∀x∈[−72,72]|x|,12≤{x}<1
    If L is number of point of discontinuity any M is the number of point on non-differentiability of the function f(x), then (L+M) is equal to

    A18
    B20
    C21
    D16

  • Consider the functions
    f(x)={x+1,x≤12x+1,1<x≤2andg(x)={x2,−1≤x<2x+2,2≤x≤3
    The domain of the function f(g(x)) is

    A[0,√2]
    B[−1,2]
    C[−1,√2]
    DNone of these

  • Consider the functions
    f(x)={x+1,x≤12x+1,1<x≤2andg(x)={x2,−1≤x<2x+2,2≤x≤3
    The range of the function f(g(x)) is

    A[1,5]
    B[2,3]
    C[1,2]∪[3,5]
    DNone of these