For all complex numbers z1,z2 satisfying |z1|=12 and |z2−3−4i|=5, find the minimum value of |z1−z2|
Video Solution
Text Solution
The correct Answer is:2
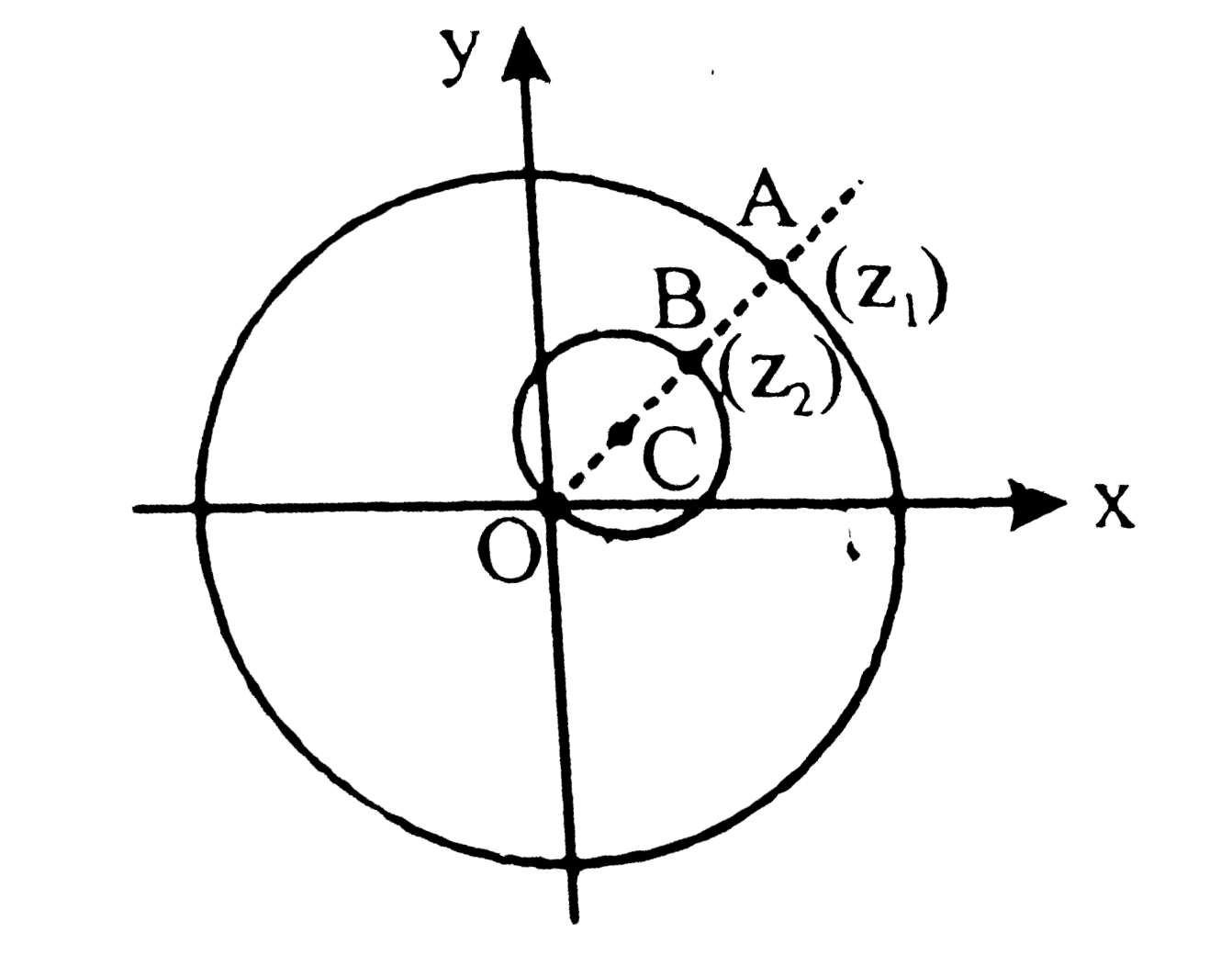
|z1|=12⇒z1lies on a circle with centre (0,0) and radius 12 units, and |z2−3−4i|=5⇒z2 lies on a circle with centre (3,4) and radius 5 units.
From the figure it is clear that |z1−z2|, that is , distance between z1 and z2 will be minimum when they lie at A and B, respectively, i.e., on diagram as shown. Then
|z1−z2|=AB=OA=12−2(5)=2
|
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Physics, SECTION-1 (PART-A)
5 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Physics, SECTION-1 (PART-A) [COMPREHENSION TYPE]
2 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Math
15 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
Knowledge Check
For all complex numbers z1,z2 satisfying |z1|=12 and |z2−3−4i|=5, find the minimum value of |z1−z2|
A0B2C7D17For all complex numbers z1andz2 satisfying |z1|=12and|z2−3−4i|=5, the minimum value of |z1−z2| is
A4B3C1D2Let z1andz2 be two complex numbers satisfying |z1|=9 and |z2−3−4i|=4 Then the minimum value of |z1−Z2| is
A1B2C√2D0
For all complex numbers z1,z2 satisfying |z1|=12and|z2−3−4i|=5 the minimum value of |z1−z2| is (A) 0 (B) 2 (C) 7 (D) 17
View SolutionFor all complex numbers z1,z2 satisfying |z1|=12 and |z2−3−4ι|=5, the minimum value of |z1−z2| is: a. 0 b. 2 c. 7 d. 17
View SolutionLet z1andz2 be two complex numberjs satisfying |z1|=3and|z2−3−4i|=4. Then the minimum value of |z1−z2| is
View SolutionFor all complex number z1,z2 satisfying |z1|=12 and |z2−3−4ι|=5,then |z2−ιz1|
View SolutionLet Z1 and Z2 be two complex numbers satisfying |Z1|=9 and |Z2−3−4i|=4. Then the minimum value of |Z1−Z2| is
View Solution
