The ellipse $4 x^{2} + 9 y^{2} = 36$ and the hyperbola $a^{2} x^{2} - y^{2} = 4$ intersect at right angles. Then the equation of the circle through the points of intersection of two conics is $x^{2} + y^{2} = 5$ $\sqrt{5} (x^{2} + y^{2}) - 3 x - 4 y = 0$ $\sqrt{5} (x^{2} + y^{2}) + 3 x + 4 y = 0$ $x^{2} + y^{2} = 25$

A

1

B

2

C

3

D

4

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, C, D

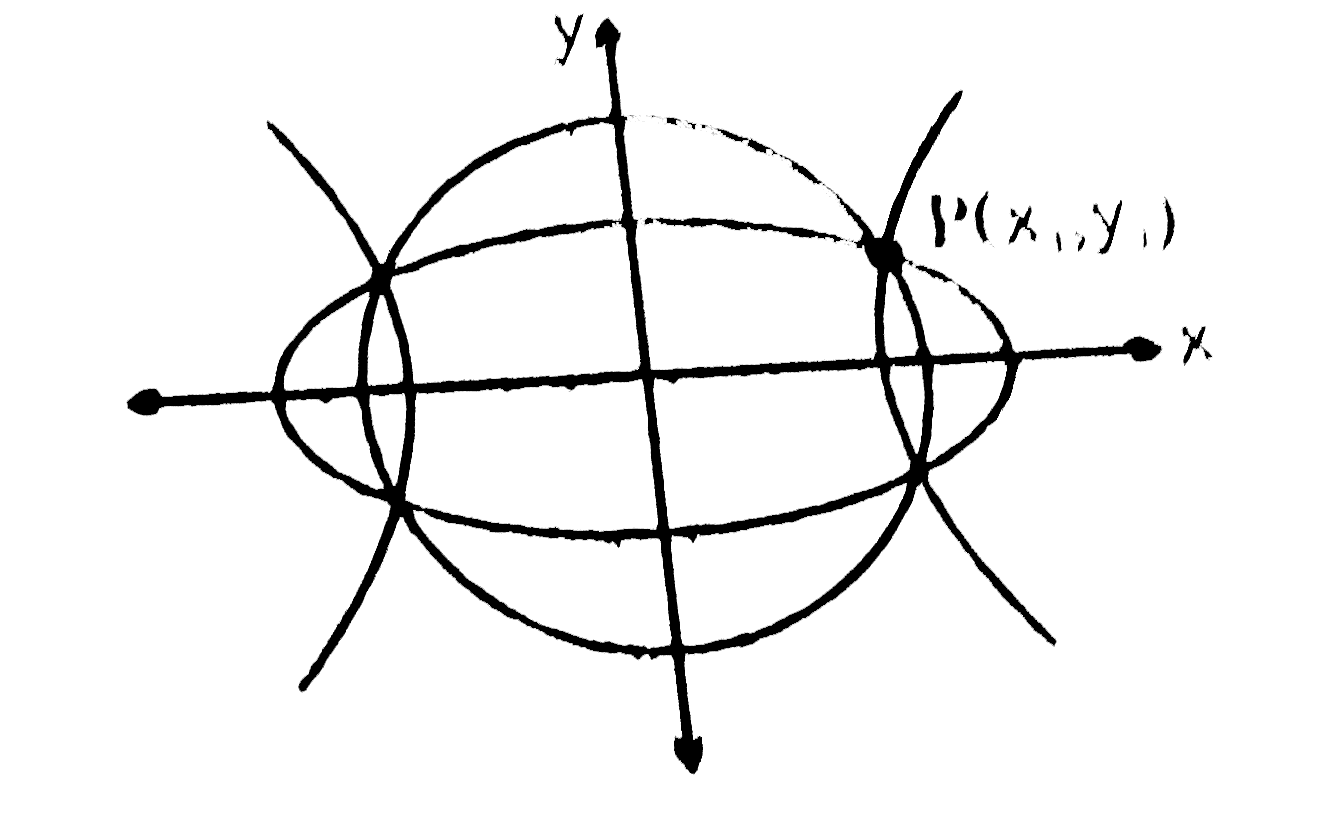
Since the ellipse and hyperbola intersect orthogonally then they are confocal.
For ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ , the foci are $(\pm \sqrt{5}, 0)$ and for hyperbola $\frac{x^{2}}{\frac{4}{α^{2}}} - \frac{y^{2}}{4} = 1$ ,
foci are $(\pm \frac{2}{α} \sqrt{1 + α^{2}}, 0)$ .
$∴ \frac{4}{α^{2}} (1 + α^{2}) = 5 \Rightarrow \frac{4}{α^{2}} + 4 = 5 \Rightarrow α^{2} = 4 \Rightarrow α = 2$ .

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The ellipse $4 x^{2} + 9 y^{2} = 36$ and the hyperbola $4 x^{2} - y^{2} = 4$ have the same foci and they intersect at right angles then the equation of the circle through the points of intersection of two conics is
A $x^{2} + y^{2} = 5$
B $\sqrt{5} (x^{2} + y^{2}) - 3 x - 4 y = 0$
C $\sqrt{5} (x^{2} + y^{2}) + 3 x + 4 y = 0$
D $x^{2} + y^{2} = 25$
Question 2 - Select One
The equation of the circle through points of intersection of the circle $x^{2} + y^{2} - 4 y + 4 = 0$ and the line x+2y=4 which touches the line $x + 2 y = 0$ , is
A $x^{2} + y^{2} + x + 2 y = 0$
B $x^{2} + y^{2} - x - 2 y = 0$
C $x^{2} + y^{2} - x + 2 y = 0$
DNone of these
Question 3 - Select One
The equation of the line passing through the intersection of the circles $3 x^{2} + 3 y^{2} - 2 x + 12 y - 9 = 0$ and $x^{2} + y^{2} + 6 x + 2 y - 15 = 0$ is
A $8 x - 10 y - 7 = 0$
B $10 x - 3 y - 27 = 0$
C $4 x + 10 y - 5 = 0$
Dnone

BANSAL-TEST PAPERS-MATHS

Home
Ask Doubt
Profile