A $(- 1, 0) and B (2, 0)$ are two given points. A point M is moving in such a way thatthe angle B in the triangle AMB remains twice as large as the angle A. Show that the locus of the pointM is a hyperbola. Find the eccentricity of the hyperbola.

A

eccentricity equals 2

B

vertices $(\pm 3, 0)$

C

length of latus-rectum equals 6

D

equation of directrices are $x = \pm \frac{1}{2}$

Video Solution

Text Solution

Verified by Experts

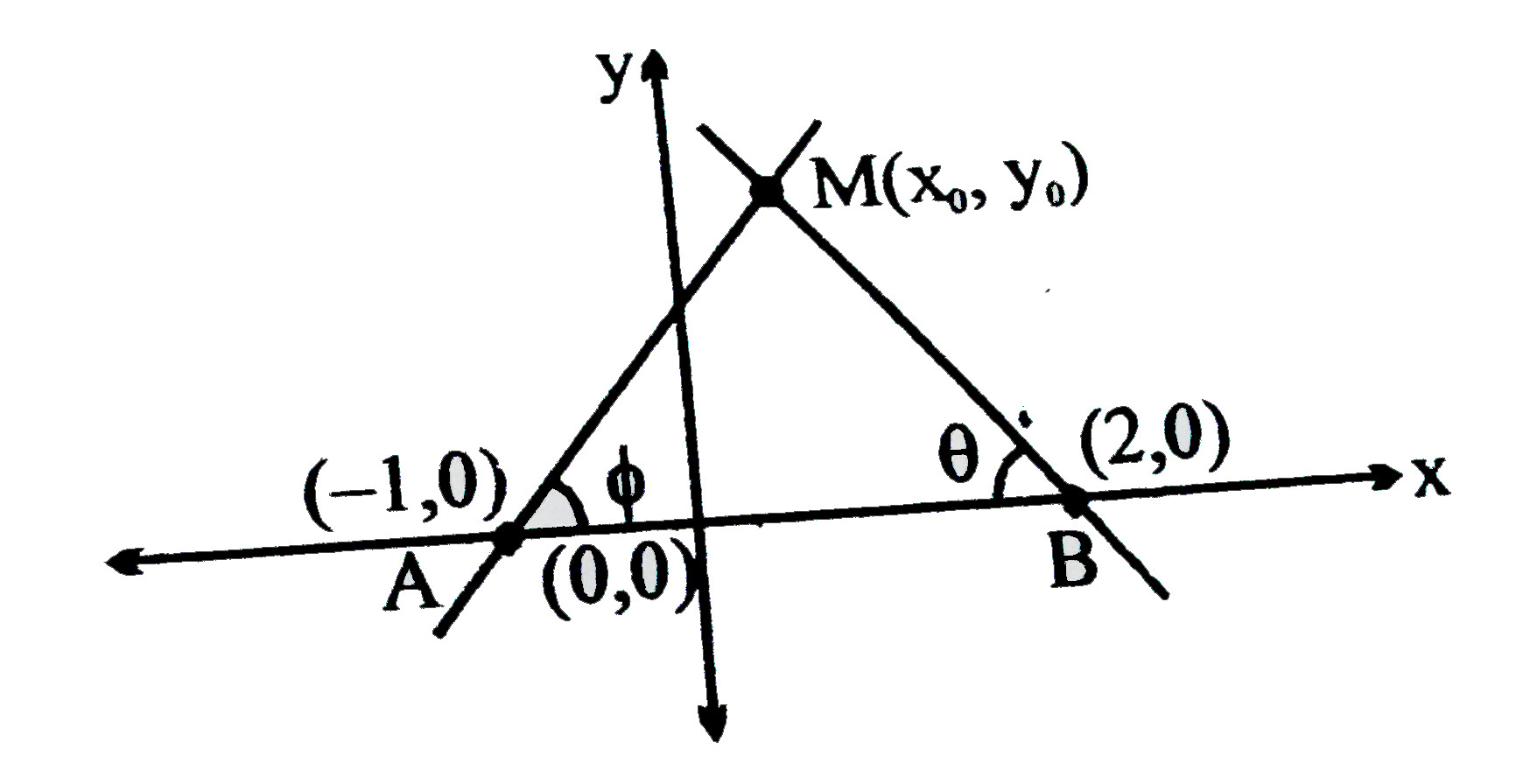
Given, $θ = 2 ϕ \Rightarrow \tan θ 2 ϕ$
$\Rightarrow \tan θ = \frac{2 \tan ϕ}{1 - \tan^{2} ϕ} \Rightarrow \frac{- y_{0}}{x_{0} - 2} = \frac{2 y_{0} (x_{0} + 1)}{{(x_{0} + 1)}^{2} - y_{0}^{2}} \Rightarrow \frac{- 1}{x_{0} - 2} = \frac{2 (x_{0} + 1)}{{(x_{0} + 1)}^{2} - y_{0}^{2}}$
$\Rightarrow 3 x_{0}^{2} - y_{0}^{2} = 3$
$∴$ Locus of M is hyperbola $3 x^{2} - y^{2} = 3$
Now, verify alternatives.

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A and B are two fixed points. The locus of a point P such that $∠ A P B$ is a right angle, is:

A $x^{2} + y^{2} = a^{2}$
B $x^{2} - y^{2} = a^{2}$
C $2 x^{2} + y^{2} = a^{2}$
DNone of these

BANSAL-TEST PAPERS-MATHS

Home
Ask Doubt
Profile