Question

Name and define elements of earth's magnetism.

Explanation

Earth has three magnetic elements :
(i) Declination
(ii) Dip or Inclination
(iii) Horizontal component of the earth.s field.
Let us consider each of them in detail.
(i) Declination. It is defined as the angle between the magnetic meridian and the geographic meridian at a place.
It is denoted by angle `theta` in Fig (a).
In Fig., let PKLM represents the magnetic meridian and PK.L.M represents the geographic meridian at the place P. Then angle `theta` between these two planes, by definition, is the angle of declination at the place P.

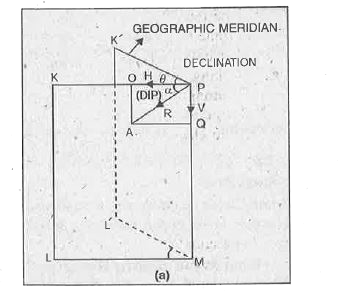
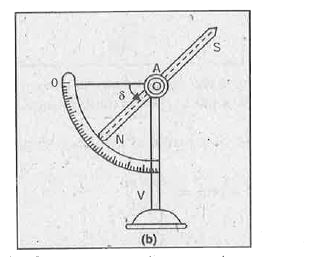
(ii) Dip or inclination `(delta)`. Dip at a place is defined as the angle between the direction of the total intensity of the earth.s magnetic field and a horizontal line in the magnetic meridian.
In Fig. (a), PA represents the total or resultant intensity of the earth.s magnetic field R in magnitude as well as in direction. As PA makes an angle `delta` with PO, the angle of dip at the place P is `delta`.
(iii) Horizontal Component (H). The total intensity of the earth.s magnetic field at any point can be resolved into two rectangular components, one along the horizontal and the other along the vertical direction.
The component of the resultant intensity of the earth.s magnetic field in the horizontal direction in magnetic meridian is called its horizontal component. It is denoted by H. The component of the resultant intensity of the earth.s magnetic field in the vertical component. It is denoted by V.

Relation between magnetic elements
In Fig. (a) the resultant intensity, i.e. R along PA has been resolved into two rectangular components. Clearly, the horizontal component is along PO
`i.e," "H=Rcosdelta" "...(1)`
and the vertical component is along PQ
`i.e," "V=Rsindelta" "...(2)`
Dividing (2) by (1), we get
`V/H=(Rsindelta)/(Rcosdelta)=tandelta" "...(3)`
Squaring (1) and (2) and adding, we get
`H^(2)+V^(2)=R^(2)(cos^(2)delta+sin^(2)delta)`
or `H^(2)+V^(2)=R^(2)`