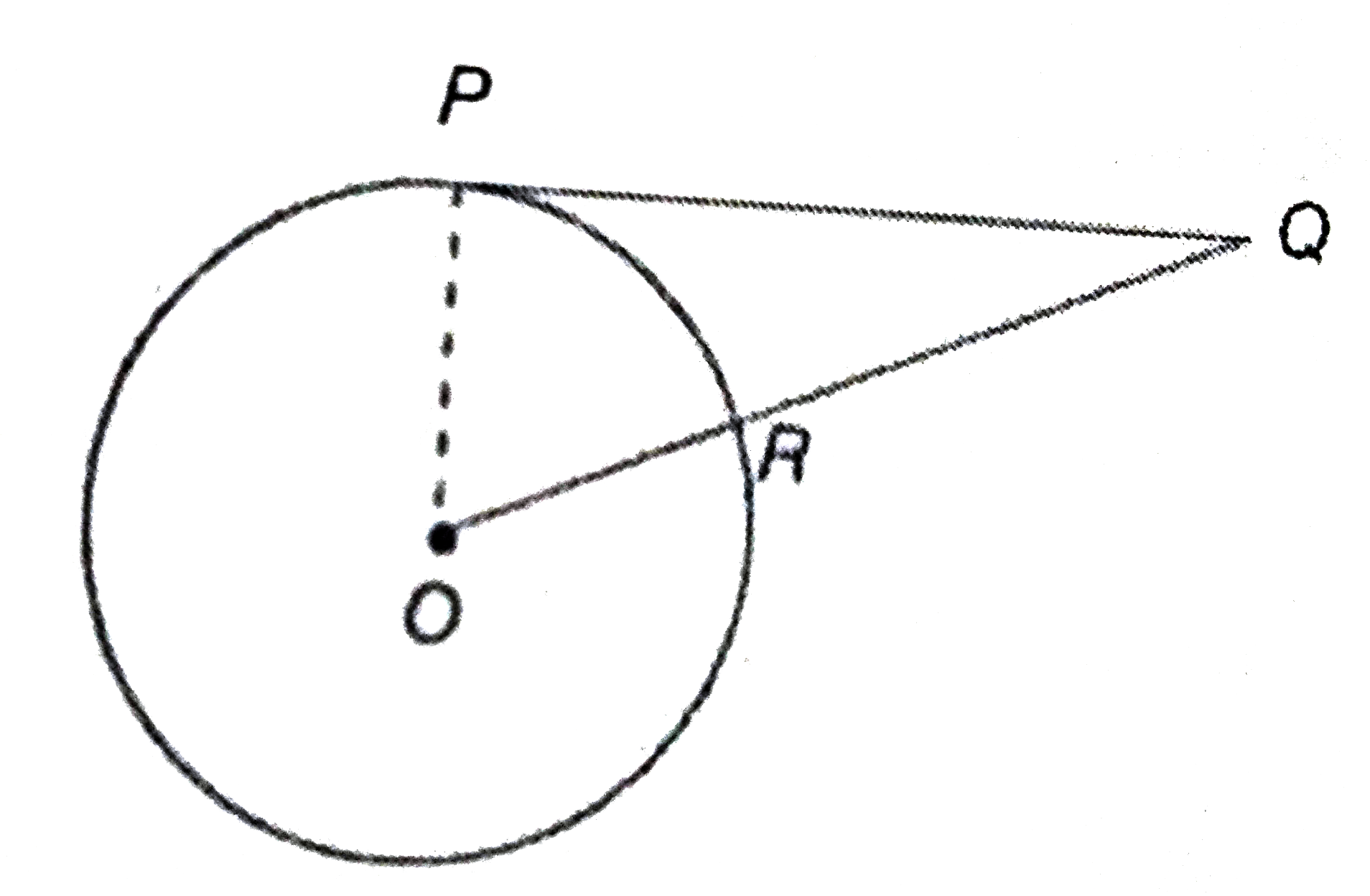
In the given figure (not to scale), PQ is a tangent segment , drawn to the circle with centre O at P and QR =RO. iF PQ=3√3cm, and ORQ is a line segment, then find the radius of the circle.
(a) √3cm
(b) 3cm
(c) 2√3cm
(d) 2cm

Let radius of the circle be x.
∴OR=RQ=x(givenOR=RQ)
Join OP
∴¯¯¯¯¯¯OP⊥¯¯¯¯¯¯PQ
OP2+PQ2=OQ2
⇒x2+(3√3)2=(2x)2
⇒3x2=27⇒x2=9⇒x=±3
But x is positive.
∴x=3cm.
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Test Yours concepts very shory answer type questions29videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Short answer type questions13videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - BANKING EXERCISE - LEVEL 310videos
BANKING
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-315videos
LIMITS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the adjoining figure, the length of BC is
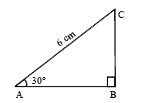
(a)2√3 cm
(b)3√3 cm
(c)4√3 cm
(d)3 cmA2√3 cmB3√3 cmC4√3 cmD3 cm - Question 2 - Select One
In the figure given, the radius of circle is (PS=12 cm, PQ=8 cm)
 A8 cmB5 cmC4 cmD10 cm
A8 cmB5 cmC4 cmD10 cm - Question 3 - Select One
In the given figure, PQ is the tangent of the circle. Line segment PR intersects the circle at N and R. PQ=15cm,PR=25cm, find PN:
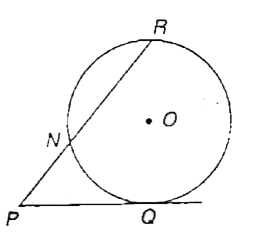 A15 cmB10 cmC9 cmD6 cm
A15 cmB10 cmC9 cmD6 cm
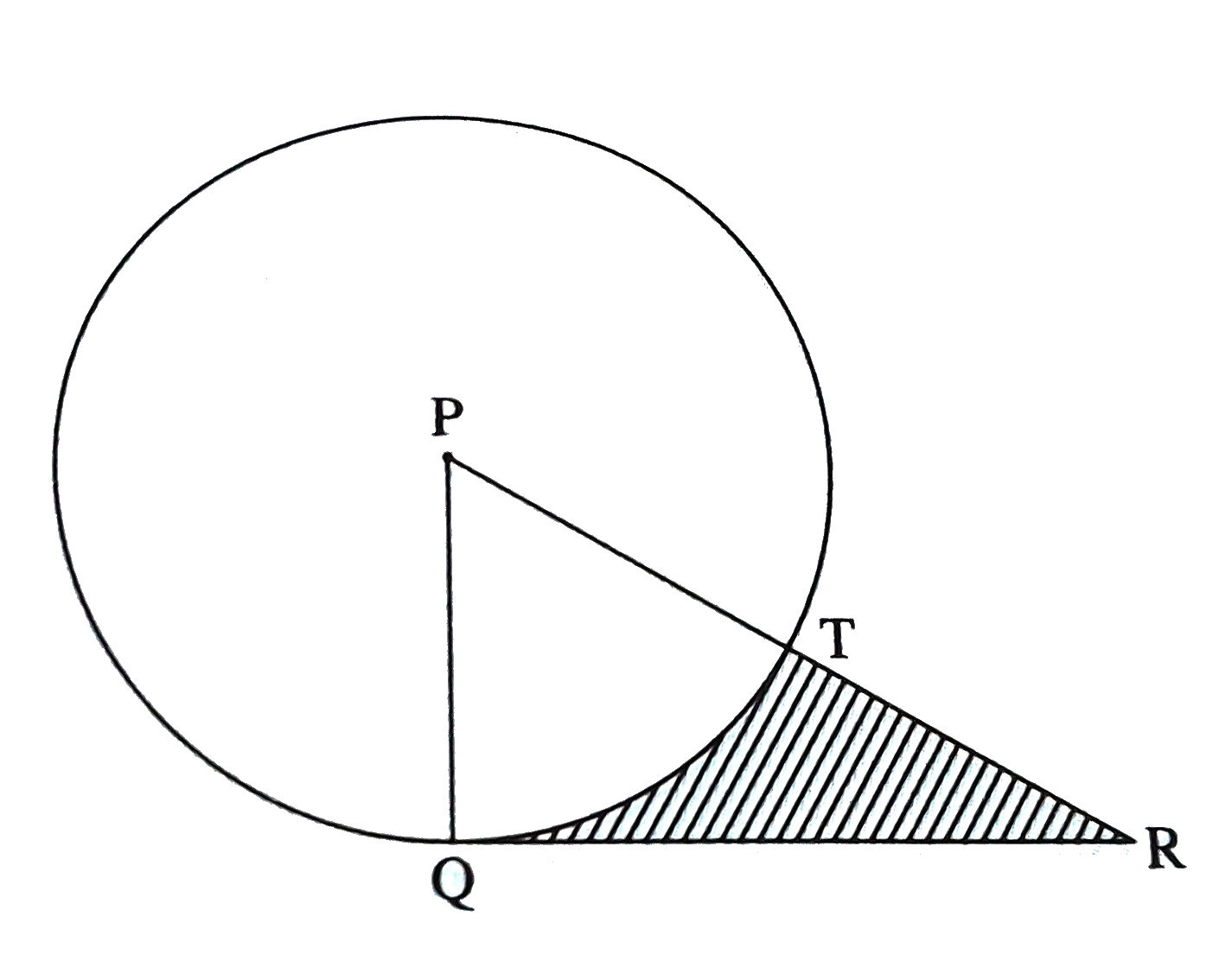
In the figure, segment QR is a tangent to the circle with centre P.PR = 12 cm and PQ = 6 cm. Find the area of shaded region. (√3=1.73,π=3.14)
 View Solution
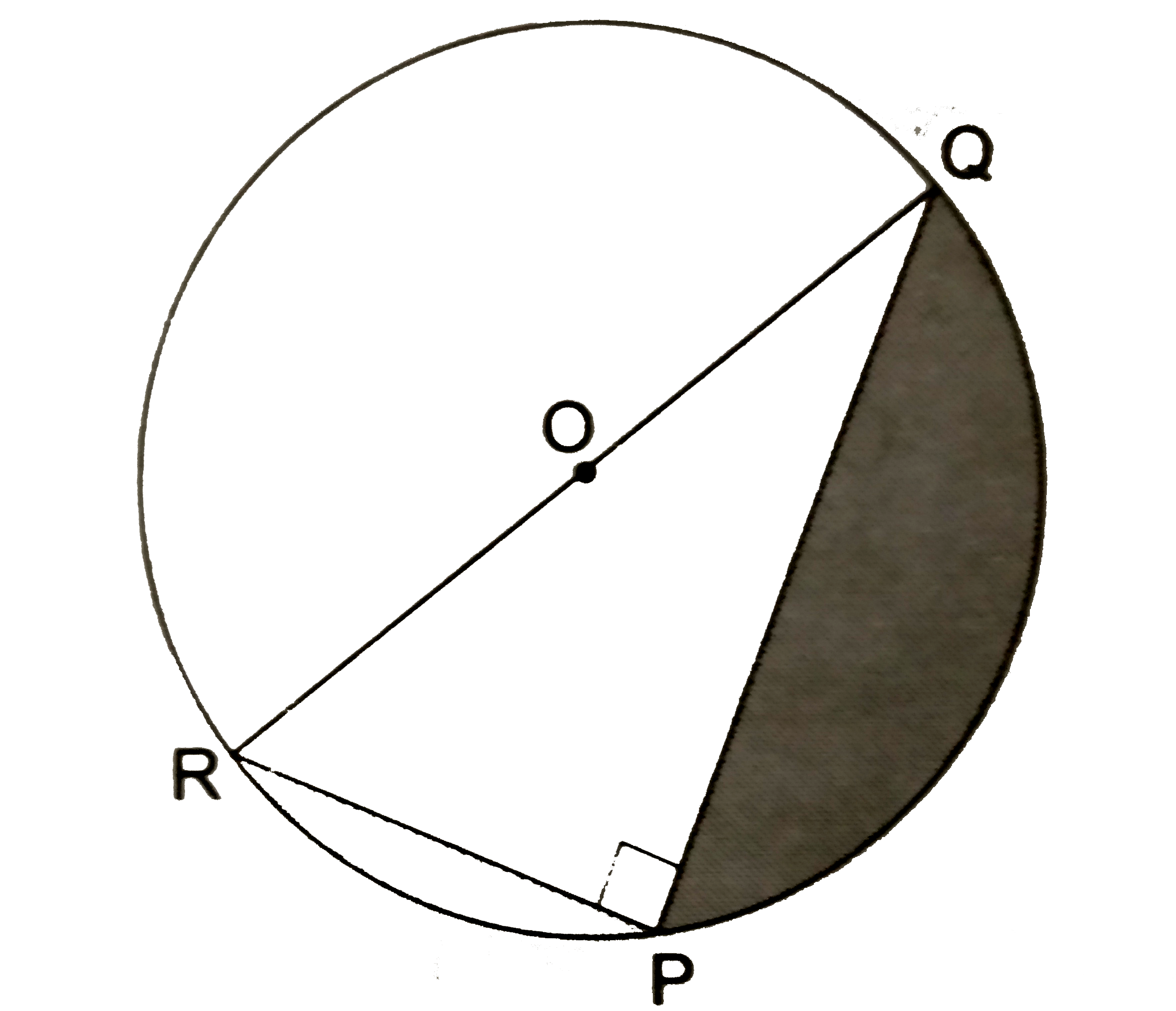
View SolutionIn the given figure, PQ = 24 cm PR = 7 cm and O is the centre of the circle. Find the area of the shaded region. (Use π=3.14)
 View Solution
View SolutionIn the given figure PQ=24cm,PR=78cm and O is the centre of the circle. Find the area of the shaded region. [Take π=3.14]
 View Solution
View SolutionPQR is a right angled triangle at Q with QR =12 a=cm and PQ=5cm. A circle with centre O is inscribed in △PQR. Find the radius of the circle.
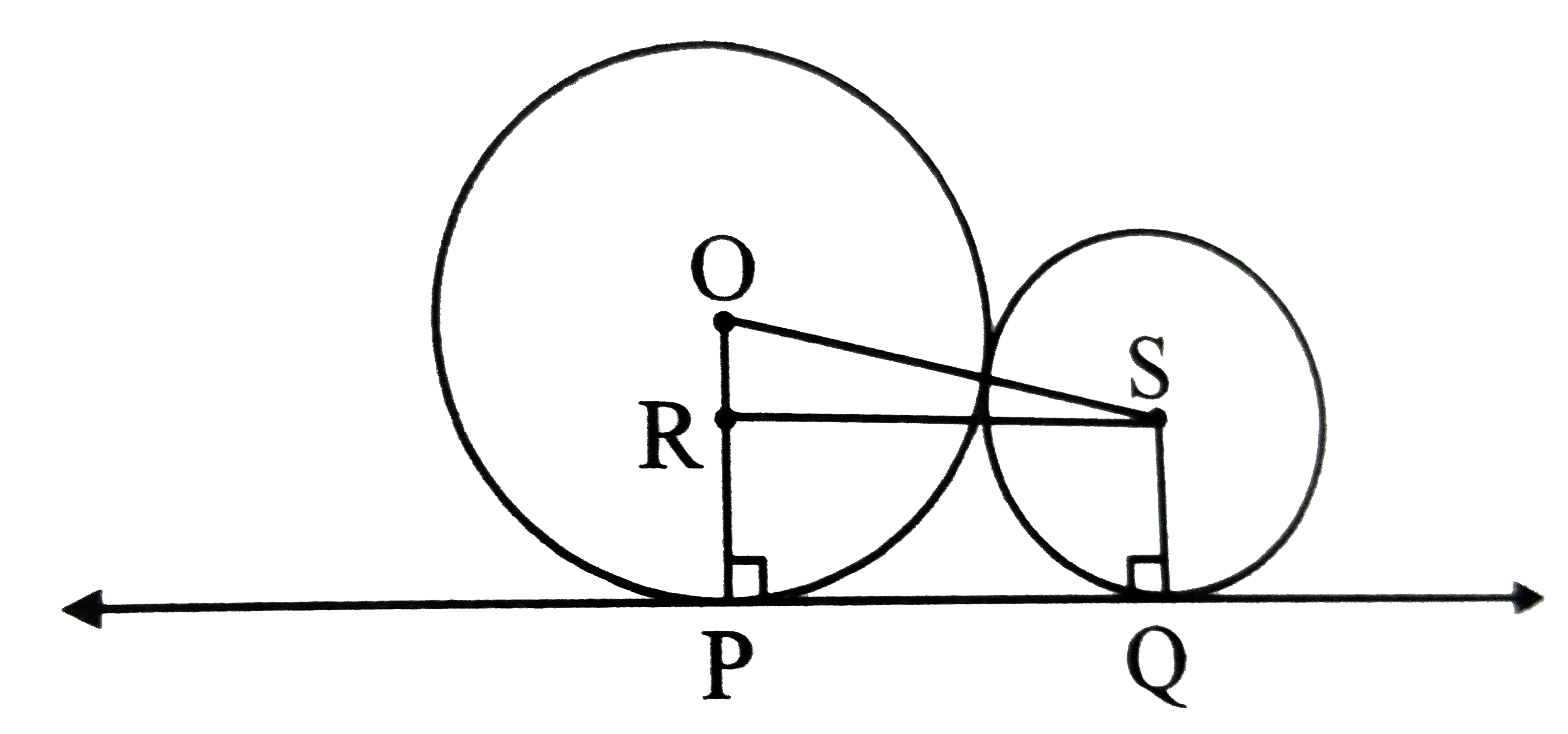
View SolutionIn the adjoining figure , line PQ is a common tangent to the externally touching circles and the radii of two circles are 25cm and 9cm. Find the length of the common tangent segment of these circles.
 View Solution
View Solution