Ar and BS are the tangents to the circle, with centre O, touching at P and Q respectively and PQ is the chord. If ∠OQP=24∘,then∠RPQ= __________.
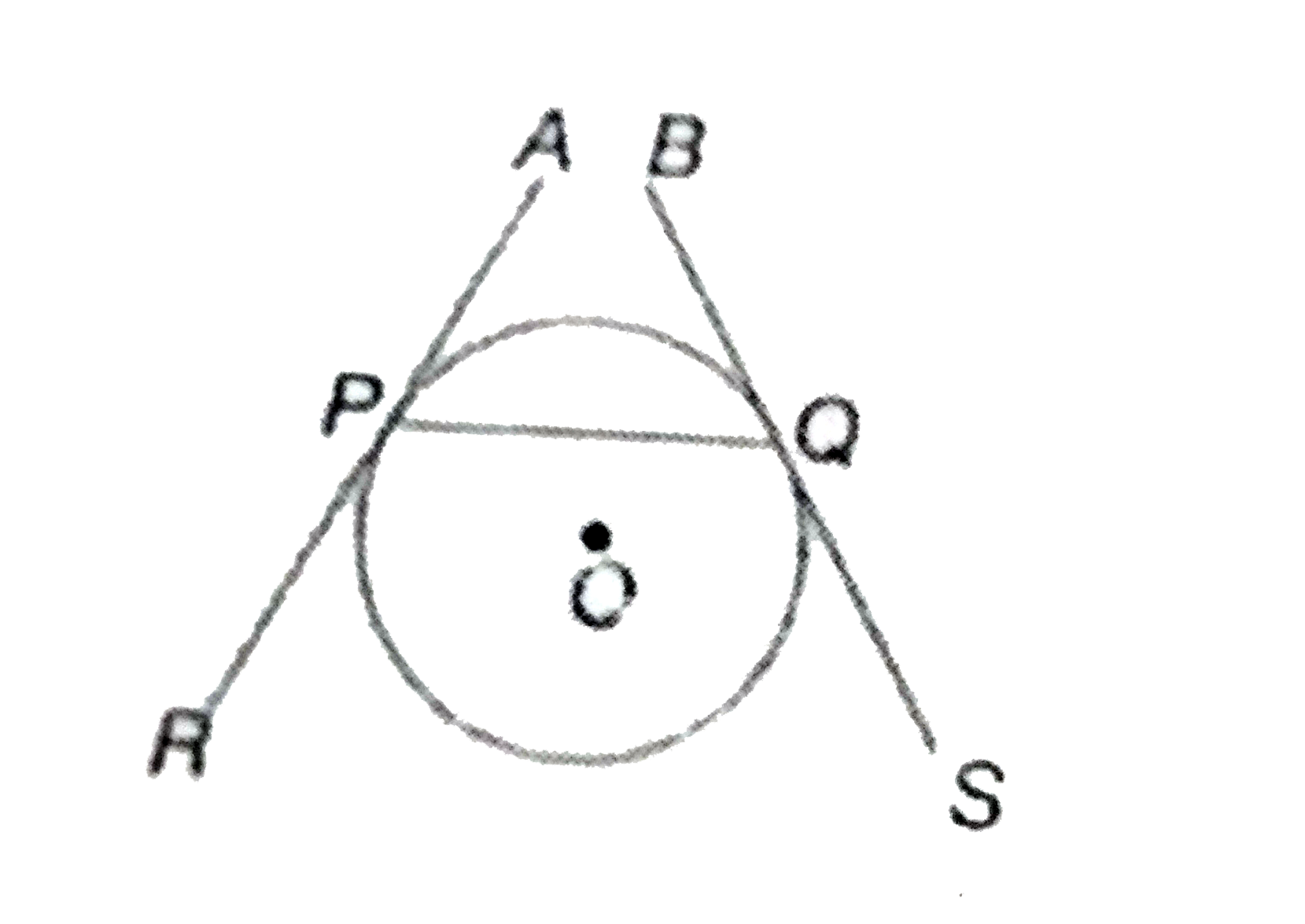
100∘
115∘
150∘
90∘
The correct Answer is:B
Radius is perpendicular to the tangent at the point of contact.
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -2
17 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -3
15 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Essay type questions
3 Videos
- BANKING BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - BANKING EXERCISE - LEVEL 3
10 Videos
- LIMITSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-3
15 Videos
Similar Questions
In the given figure, PQL and PRM are tangents to the circle with centre 'O' at the points Q and R, respectively and S is a point on the circle such that ∠SQL=50∘and∠SRM=60∘. Then ∠QSR is equal to
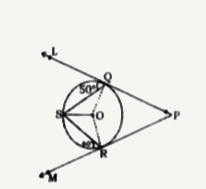
View SolutionThe sides AB,BC and AC of a triangle ABC touch a circle with centre O and radius r at P, Q, and R respectively.
View Solution
Knowledge Check
In the given figure, O is the centre of the circle . AC and AB are the tangents to the circular at points P and Q , respectively. Also ∠RPC=55∘and∠RQB=60∘ then ∠PRQand∠QAP are, respectively .
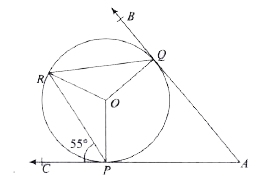 A50∘B60∘C30∘D40∘
A50∘B60∘C30∘D40∘If PQ and PR are two tangents to ta circle with centre O. if ∠QPR=46∘, then ∠QOR is equal to
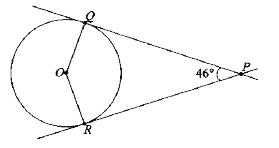 A67∘B46∘C44∘D134∘
A67∘B46∘C44∘D134∘Two circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
A65B130C195D135
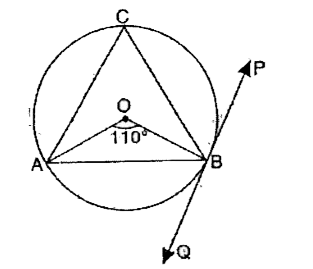
In figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to
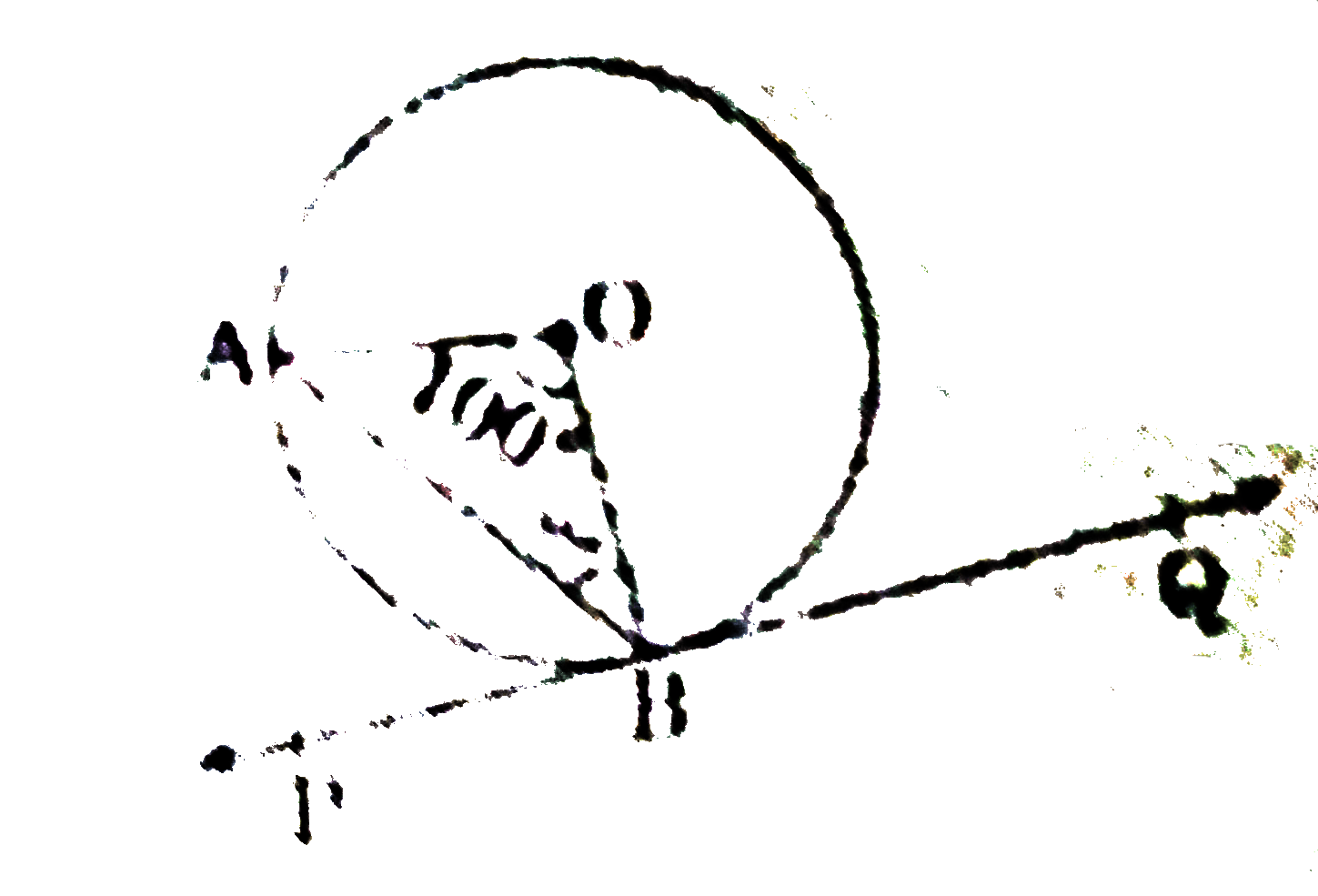
View SolutionIn the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
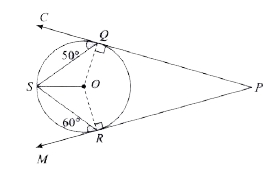
View SolutionIn the figure , PQ and PR are tangent to the circle with centre O. Also, S is a point on the circle such that ∠SQC=50∘and∠SRM=60∘, then ∠QSR=
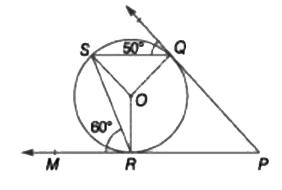
View SolutionIn the figure, O is the centre of a circle,PQL and PRM are the tangents at the points Q and R respectively and Sis a point on the circle such that ∠SQL=50∘and∠SRM=60∘. Then , ∠QSR is equal to
View SolutionPQ is tangent at a point R of the circle with centre O. If ST is a diameter of the circle and ∠TRQ=30∘ find ∠PRS
View Solution
