In the following figure, O is the centre of the circle and D. E and F are mid-points of AB,BO and OA respectively . If ∠DEF=30∘. Then find ∠ACB.
A
30∘
B
60∘
C
90∘
D
120∘
Text Solution
The correct Answer is:B
(i) ADEF is a parallelogram.
(ii) ∠FAD=30∘and∠OAD=∠OBA
(angles opposite to equal sides).
|
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -2
17 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -3
15 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Essay type questions
3 Videos
- BANKING BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - BANKING EXERCISE - LEVEL 3
10 Videos
- LIMITSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-3
15 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle. AB is tangent. AB=12cmandOB=13cm. Find OA:
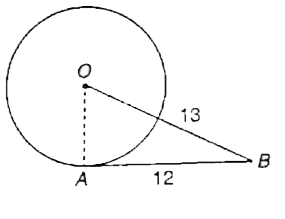A6.5 cmB6 cmC5 cmDnone of theseIn the given figure, O is the centre of the circle . AC and AB are the tangents to the circular at points P and Q , respectively. Also ∠RPC=55∘and∠RQB=60∘ then ∠PRQand∠QAP are, respectively .
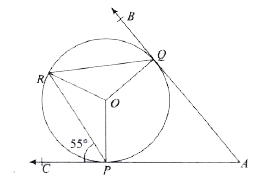A50∘B60∘C30∘D40∘In the given figure, O is the centre of the circle, ∠ACB=54∘ and BCF is a straight line. Find x.
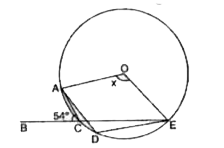A126∘B54∘C108∘D90∘
In the diagram , O is the centre of the circle and ∠OPA=30∘, Find ∠ACBand∠ADB respectively.
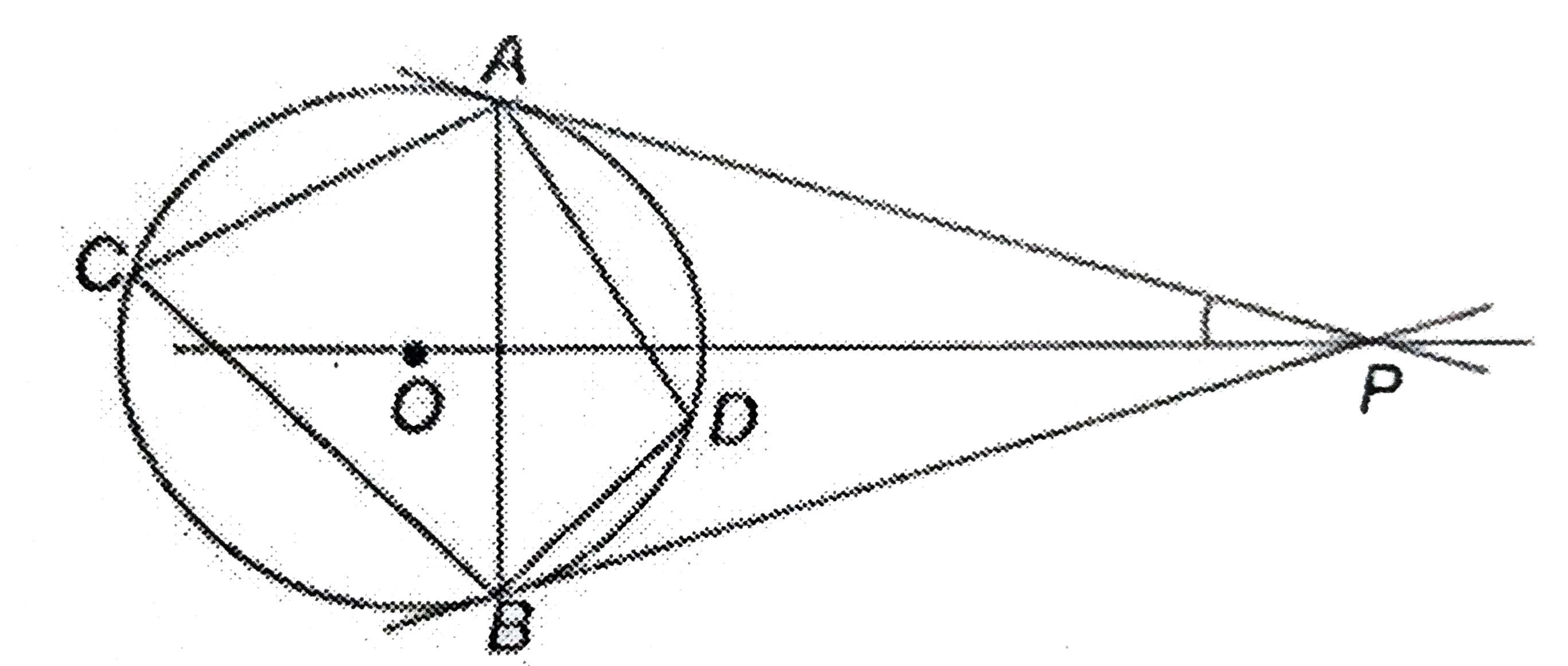
View SolutionIn the following figure, AB is an arc of the circle, C and D are the points on the circle. If ∠ACB=30∘, Find ∠ADB.
View SolutionIn the following figure, O is the centre of the circle. AB is an arc of the circle, such that ∠AOB=80∘.Find ∠ACB.
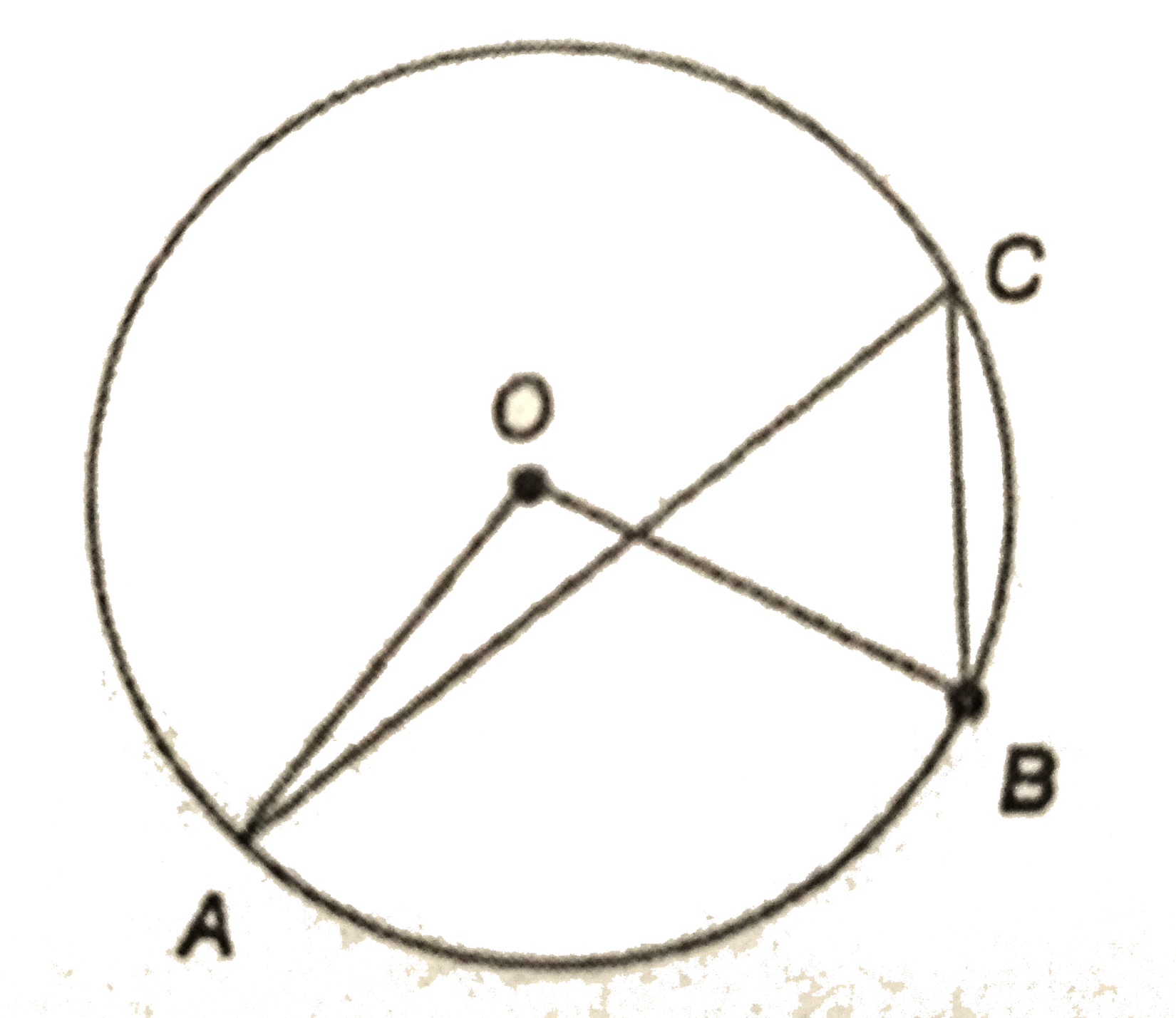
View Solution
In the figure (not to scale ), O is the centre of the circle and ∠OBA=30∘. Find ∠ACB
View SolutionIn the following fiure. O is the centr of the circle and AD is the diameter. If ∠ACB=135∘ , then find ∠DOB.
View Solution