In the following figure, two circles X and Y with centres A and B respectively intersect at C and D. The radii AC and AD of circle X are tangents to the circle Y. Radii BC and BD of circle Y are tangents to the circle X. find ∠AEC.

45∘
60∘
90∘
Cannot be determined
The correct Answer is:C
Recall the properties of a kite.
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -2
17 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -3
15 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Essay type questions
3 Videos
- BANKING BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - BANKING EXERCISE - LEVEL 3
10 Videos
- LIMITSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-3
15 Videos
Similar Questions
Two circles with radii a and b respectively touch each other externally . Let c be the radius of a circle that touches these two circles as well as a common tangent to the circles. Then
View SolutionFind the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR=110∘
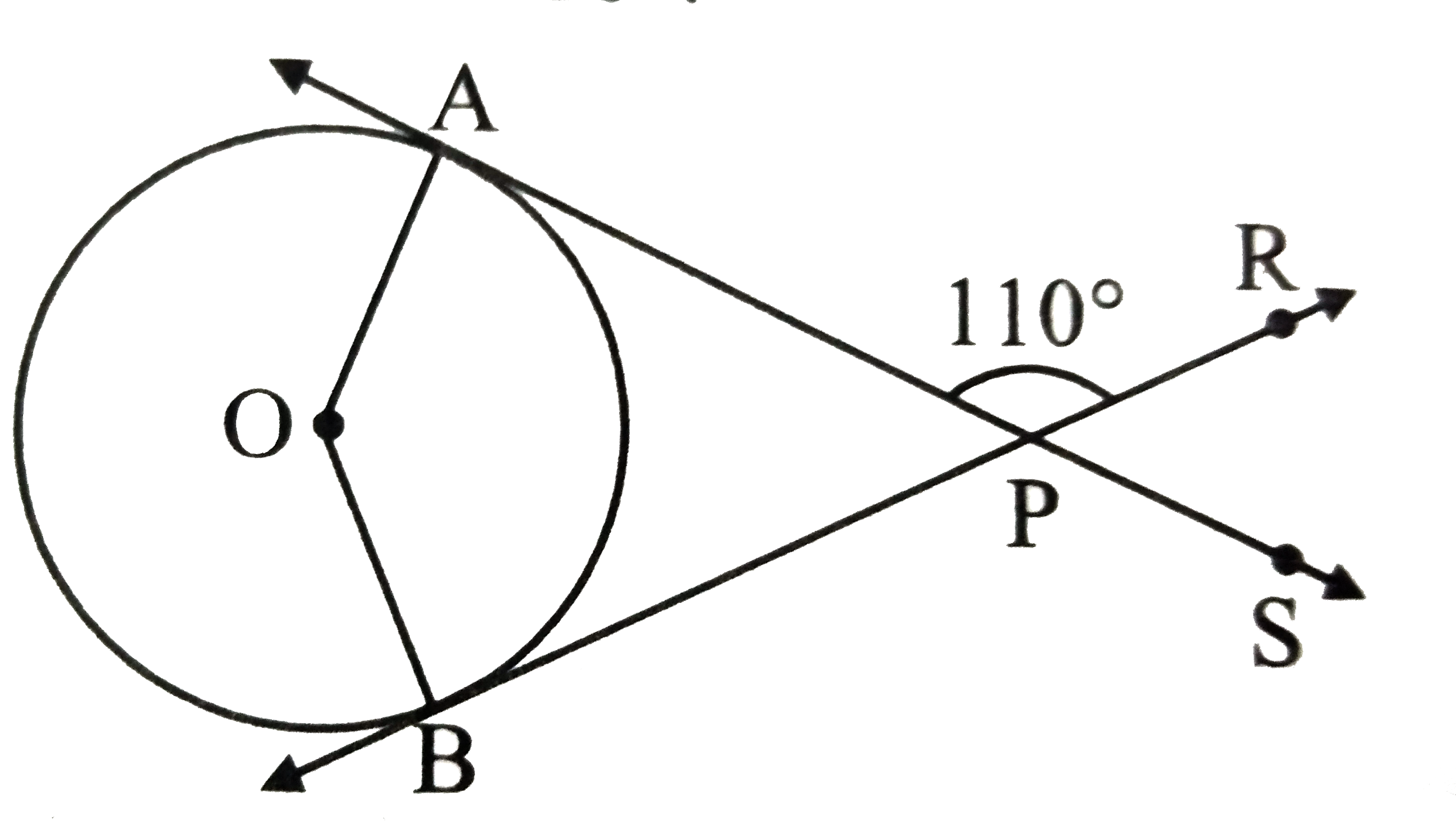
View Solution
Knowledge Check
Two circles with centres A and B of radii 3 cm and 4 cm respectively intersect at two points C and D, such that AC and BC are tangents to the two circle. Find the length of the common chord CD.
A4.2 cmB8.4 cmC2.4 cmD4.8 cmTwo circles with centres A and B of radii 3 cm and 4 cm respectively intersect at two points C and D, such that AC and BC are tangents to the two circle. Find the length of the common chord CD.
A4.2 cmB8.4 cmC2.4 cmD4.8 cmTwo circles with centres A and B of radii 3 cm and 4 cm respectively intersect at two points C and D, such that AC and BC are tangents to the two circle. Find the length of the common chord CD.
A5 cmB4.8 cmC5.8 cmD3.8 cm
A circle C is tangent to the x and y axis in the first quadrant at the points P and Q respectively. BC and AD are parallel tangents to the circle with slope –1. If the points A and B are on the y-axis while C and D are on the x-axis and the area of the figure ABCD is 900 . √2 sq. units then find the radius of the circle.
View SolutionThe line 2x - y + 1 = 0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x-2y = 4. The radius of the circle is :
View SolutionThe line 2x−y+1=0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x−2y=4. The radius of the circle is
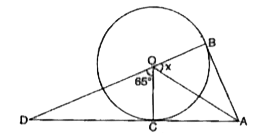
View SolutionIn the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
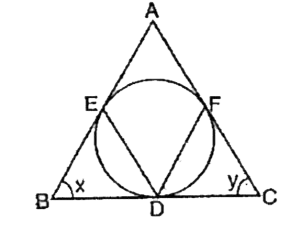
View SolutionBC, AB and AC are tangents to the circle at D, E and F respectively. ∠EBD=x∘,∠FCD=y∘. Then ∠ EDF equals
View Solution
