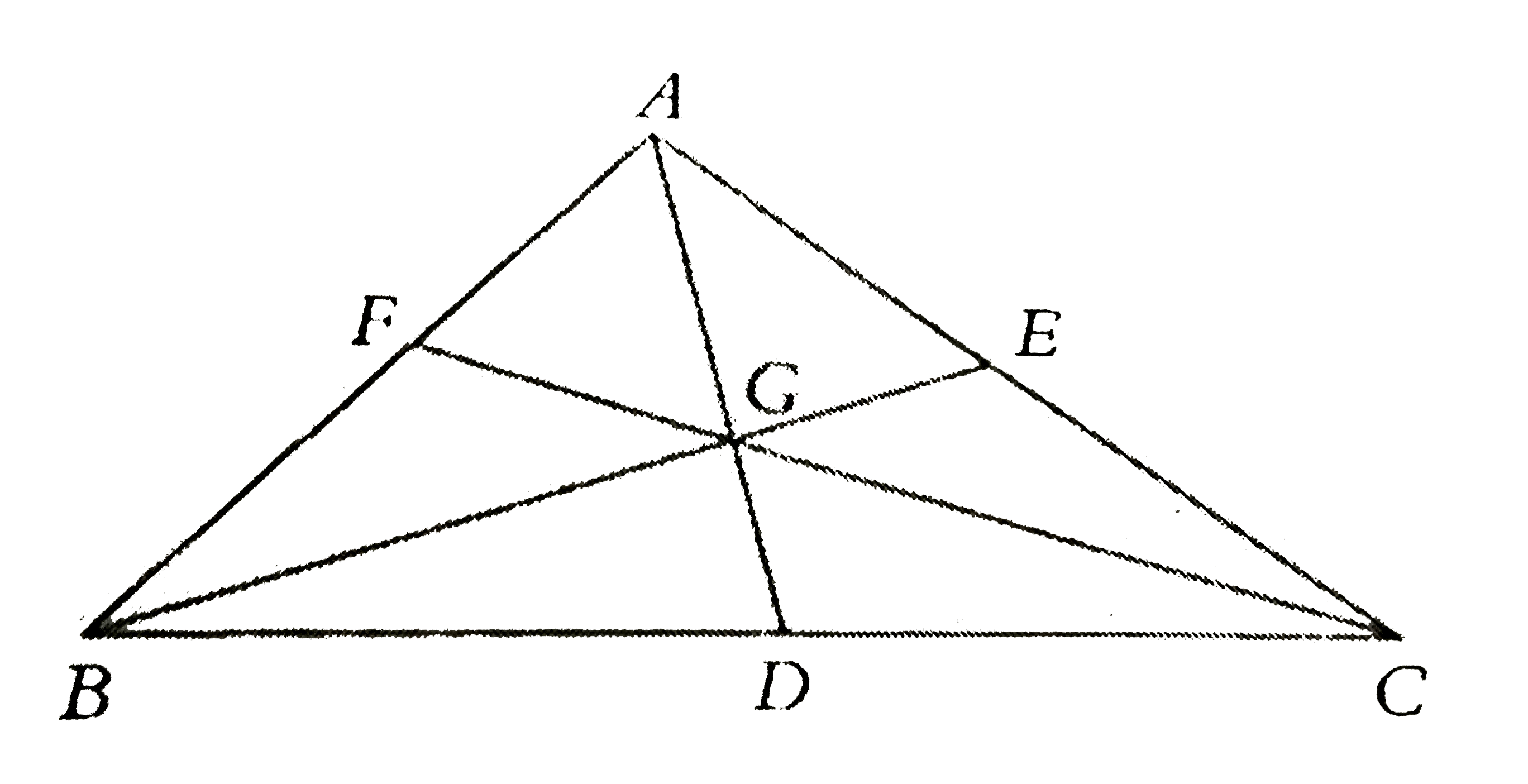
In the above $Δ A B C, ¯ ¯¯¯¯ ¯ A D, ¯ ¯¯¯¯ ¯ B E, and ¯ ¯¯¯¯ ¯ C F$ are the medians. G is the centroid. What is the ratio of the areas of $Δ B G D and Δ G C E$ ?

Video Solution

Text Solution

Verified by Experts

The three medians divide the triangle into six triangles of equal areas. Hence, the ratio of the area of $Δ B G D$ to that of $D e l T a G C E$ is 1:1.

|

Updated on:21/07/2023

Class 7 MATHS GEOMETRY

Topper's Solved these Questions

BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - very Short answer Type Question
25videos
GEOMETRY
BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Short answer Type Question
29videos
GEOMETRY
BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FORMULASEXERCISE - ASSESSMENT TESTS (Test 2)
8videos
FORMULAS
BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -2
12videos
INDICES

Similar Questions

Knowledge Check

Question 1 - Select One
In $Δ A B C$ , the medians AD and BE meet at G. The ratio of the areas of $Δ B D G$ and the quadrilateral GDCE is :
A $1 : 2$
B $1 : 3$
C $2 : 3$
D $3 : 4$
Question 2 - Select One
If G is the centroid of $Δ$ ABC, then $¯ ¯¯¯¯ ¯ C A + ¯ ¯¯¯¯ ¯ C B$ =
A3 $¯ ¯¯¯¯ ¯ G C$
B3 $¯ ¯¯¯¯ ¯ C G$
C3 $¯ ¯¯¯¯ ¯ A B$
D3 $¯ ¯¯¯¯ ¯ G A$
Question 3 - Select One
In a $Δ A B C$ , G is centroid and AD, BE, CF are medians. Find the area of quadrilateral BDGF, if the area of $Δ A B C = 72 c m^{2}$
A12
B16
C24
D8

PEARSON IIT JEE FOUNDATION-GEOMETRY -Test-2

Home
Ask Doubt
Profile