Derive the expression for the radius of the orbit of the electron and its velocity using Bohr atom model. Solution in Tamil
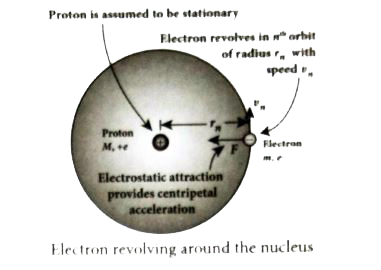
Radius of the orbit of the electron and velocity of the electron : Consider an atom which contains the nucleus at rest and an electron revolving around the nucleus in a circular orbit of radius rn as shown in figure. Nucleus is made up of protons and neutrons. Since proton is positively charged and neutron is electrically neutral, the charge of a nucleus is purely the total charge of protons.
Let Z be the atomic number of the atom, then +Ze is the charge of the nucleus. Let -e be the charge of the electron. From Coulomb.s law, the force of attraction between the nucleus and the electron is
→Fcoloumb=14πε0(+Ze)(e)r2nˆr
=−14πε0Ze2r2nˆr
This force provides necessary centripetal force
→Fcentripetal=mv2nrnˆr
where m be the mass of the electron that moves with a velocity vn in a circular orbit. Therefore ,
∣∣→Fcoloumb∣∣=∣∣→Fcentripetal∣∣
14πε0Ze2r2n=mv2nrn
rn=4πε0(mvnrn)2Zme2...(1)
From Bohr.s assumption, the angular momentum quantization condition, mvnrn=In=nh.
∴rn=4πε0(mvnrn)2Zme2
rn=4πε0(nh)2Zme2=4πε0n2h2Zme2
rn=(ε0h2πme2)n2Z(∴h=h2π) ...(2)
where n ∈N. Since ε0,h,e and π are constants. Therefore , the radius of the orbit becomes
rn=a0n2Z
where a0=ε0h2πme2=0.529 Å. This is known as Bohr radius which is the smallest radius of the orbit in an atom . Bohr radius is also used as unit of length called Bohr. 1Bohr =0.53 Å.For hydrogen atom (Z=1) , the radius of nth orbit is
rn=a0n2
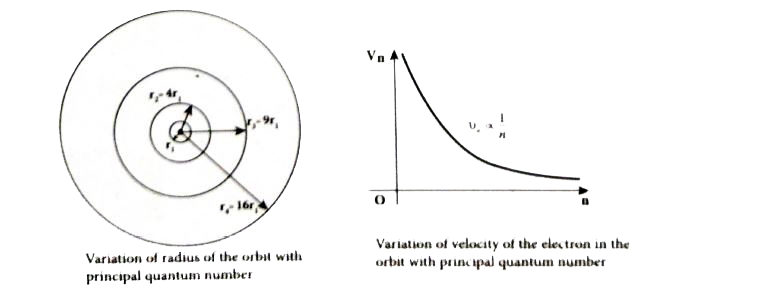
For the first orbit (ground state ),
r1=a0=0.529 Å
For the second orbit (first excited state),
r2=4a0=2.116 Å
For the third orbit (second excited state) ,
r3=9a0=4.761 Å and so on.
Thus the radius of the orbit from centre increases with n, this is rn∝n2 as shown in figure . Further, Bohr.s angular momentum quantization condition leads to
mvnrn=mvna0n2=nh2π
vn=h2πma0Zn
vn∝1n
Note that the velocity of electron decreases as the principal quantum number increases as shown in figure. This curve is the rectangular hyperbola. This implies that the velocity of electron in ground state is maximum when compared to excited states.
Topper's Solved these Questions
- SAMPLE PAPER-1 (SOLVED)Book:FULL MARKSChapter:SAMPLE PAPER-1 (SOLVED)Exercise:Questions
Explore 28 Videos
- SAMPLE PAPER-07 (SOLVED )Book:FULL MARKSChapter:SAMPLE PAPER-07 (SOLVED )Exercise:(PART - IV)(Answer all the questions.)
Explore 10 Videos
- SAMPLE PAPER-16 (UNSOLVED)Book:FULL MARKSChapter:SAMPLE PAPER-16 (UNSOLVED)Exercise:PART-IV
Explore 10 Videos
Similar Questions
What is meant by Fraunhofer lines?
View SolutionCalculate the electric field due to a dipole on its equatorial plane. (OR) Electric field due to an electric dipole at a point on the equatorial plane
View SolutionDerive an expression for electrostatic potential energy of the dipole in a uniform electric field .
View Solutionबोर मॉडल के अनुसार हाइड्रोजन परमाणु की n वीं कक्षा में इलेक्ट्रॉन के वेग का व्यंजक प्राप्त कीजिए |
View SolutionUsing Bohr's postulates of the atomic model, derive the expression for radius of n-th electron orbit. Hence obtain the expression for Bohr's radius.
View SolutionDerive the energy expression for hydrogen atom using Bohr atom model.
View SolutionDerive the expression for the radius of the orbit of the electron and its velocity using Bohr atom model.
View SolutionDerive the energy expression for hydrogen atom using Bohr atom model.
View SolutionDerive the energy expression for hydrogen atom using Bohr atom model.
View SolutionUsing Bohr's atomic model, derive the expression for the radius of nth orbit of the revolviting electron in a hydrogen atom.
View SolutionDerive an expression for the radius of nth Bohr's orbit of hydrogen atom hence write the expression for the radius of first orbit of hydrogen atom.
View SolutionUsing Bohr's postulates of the atomic model, derive the expression for radius of th electron orbit. Thus, obtain the expression of Bohr's radius.
View SolutionUsing Bohr's postulates of the atomic model. Derive the expression for radius of nth electron orbit, thus obtaining the expression for Bohr's radius.
View SolutionThe electric current I created by the electron in the ground state of H atom bohr model in terms of bohr radius (a0) and velocity of electron in first orbit v0 is
View SolutionState Bohr’s postulates for atomic model and derive an expression for radius of the electron in an orbit.
View Solution